Предмет: Математика,
автор: Аноним
336 а ,337 а ,338 а ,339 а.
Приложения:
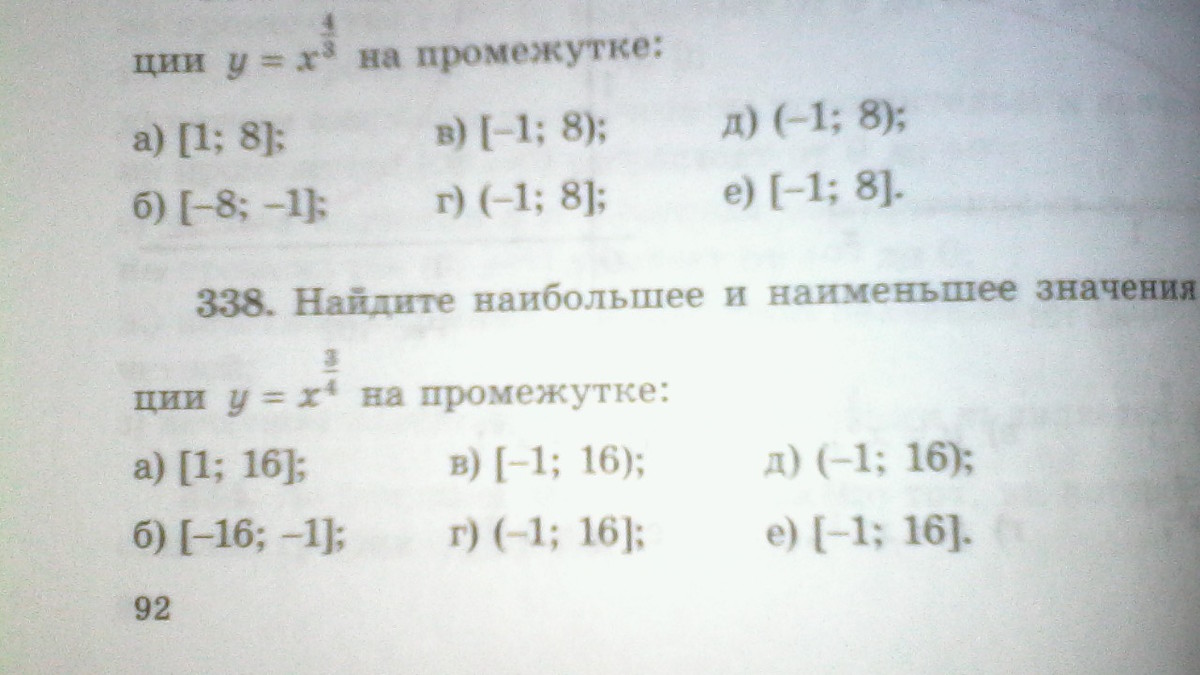


Ответы
Автор ответа:
0
336 а)
y = , x ∈ [-0,125;2]
, x ∈ [-0,125;2]
Функция не существует при х = 0 -- уходит в -оо при приближении к нулю слева и в +оо при приближении к нулю справа.
Поэтому установить min y и max y в данном случае невозможно
337 а)
y = , x ∈ [1;8]
, x ∈ [1;8]
y' = ·
· > 0 при x ∈ [1;8] -- функция растёт на данном промежутке.
> 0 при x ∈ [1;8] -- функция растёт на данном промежутке.
Поэтому:
min y = y (1) = = 1
= 1
max y = y (8) = = 16
= 16
338 а)
y = , x ∈ [1;16]
, x ∈ [1;16]
y' = ·
· > 0 -- функция растёт на всей области определения.
> 0 -- функция растёт на всей области определения.
Поэтому:
min y = y (1) = = 1
= 1
max y = y (16) = = 8
= 8
y =
Функция не существует при х = 0 -- уходит в -оо при приближении к нулю слева и в +оо при приближении к нулю справа.
Поэтому установить min y и max y в данном случае невозможно
337 а)
y =
y' =
Поэтому:
min y = y (1) =
max y = y (8) =
338 а)
y =
y' =
Поэтому:
min y = y (1) =
max y = y (16) =
Автор ответа:
0
Фотография для 339 а) нечёткая. Из того, что можно разобрать, её условие, а значит, и решение полностью совпадает с 338 а)!
Похожие вопросы
Предмет: Русский язык,
автор: liponokioj
Предмет: Обществознание,
автор: zanuraluba
Предмет: Биология,
автор: aleksandr10052009
Предмет: Биология,
автор: kissa514
Предмет: Математика,
автор: yanikdotki