Предмет: Алгебра,
автор: ddddd22
Помогите решить хоть что-нибудь
Приложения:


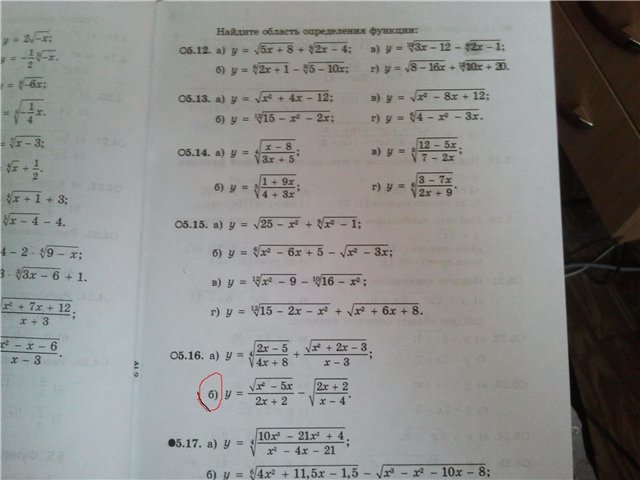
Ответы
Автор ответа:
0
6.28г
7.18a
7/18б
5.16б
x∈(-∞;-1)U[5;+∞)
Похожие вопросы
Предмет: Литература,
автор: aidabakyt08
Предмет: Математика,
автор: sofiashagbanova
Предмет: Русский язык,
автор: ponomarevairina
Предмет: География,
автор: uchenik723