Question

около правильной треугольной пирамиды со стороной основания 9 см и высотой 10 см описан шар. найдите радиус шара

Answer 1

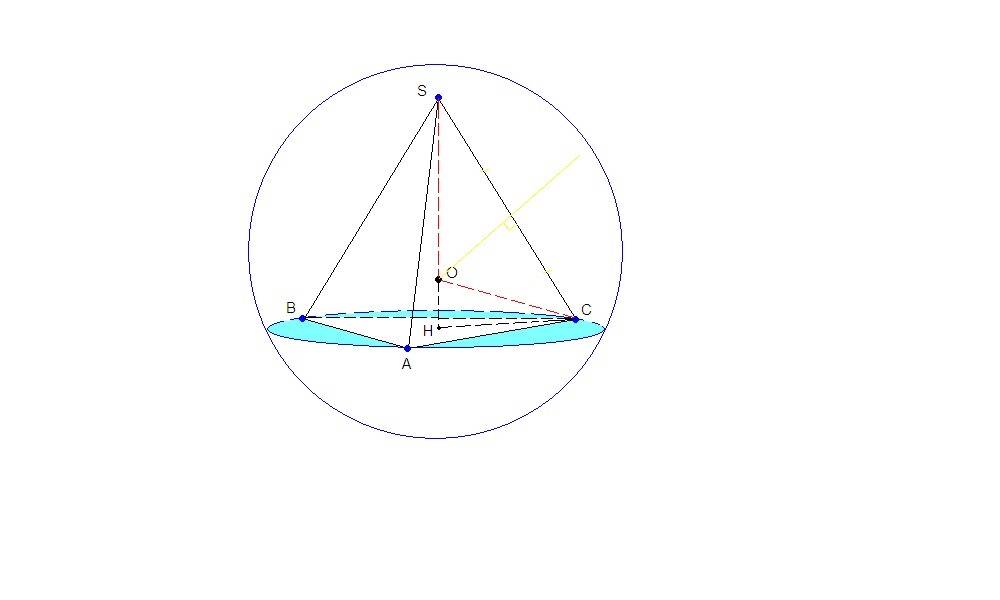
Шар описан около пирамиды, значит основание пирамиды вписано в круг - сечение шара, Н - центр основания и центр сечения, НС - радиус сечения.

Радиус окружности, описанной около правильного треугольника:

r = a√3/3, где а - сторона треугольника.

CH = AB√3/3 = 9√3 / 3 = 3√3 см.

Центр шара - точка О - лежит на пересечении высоты пирамиды и серединного перпендикуляра к ее ребру.

SO = OC = R - радиус шара.

OH = SH - SO = 10 - R

ΔOHC: ∠OHC = 90°, по теореме Пифагора

CO² = OH²+ CH²

R² = (10 - R)² + 27

R² = 100 - 20R + R² + 27

20R = 127

R = 6,35 см