Предмет: Алгебра,
автор: VikaBuldygina
Докажите четность функции:
а) y=7cos4x+3x^2
б) y=x^2-x/x+1 - x^2+x/x-2
Ответы
Автор ответа:
0
Функция является четной, если выполняется условие:

Проверим это условие, подставив в выражение (-x)
a)
 - является четной
- является четной
b)
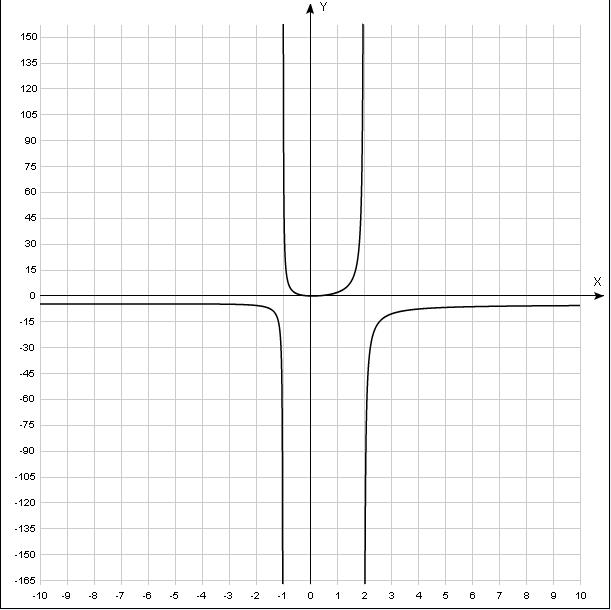
 - не является четной, график в подтверждение (видно, что график НЕ симметричен относительно оси Оу)
- не является четной, график в подтверждение (видно, что график НЕ симметричен относительно оси Оу)
Проверим это условие, подставив в выражение (-x)
a)
b)
Приложения:
Похожие вопросы
Предмет: Физика,
автор: ushlerbothongo
Предмет: Математика,
автор: anzelikakanybekova5
Предмет: Химия,
автор: edik55502oziknz
Предмет: Биология,
автор: Vfndttdf2013
Предмет: Биология,
автор: Аноним