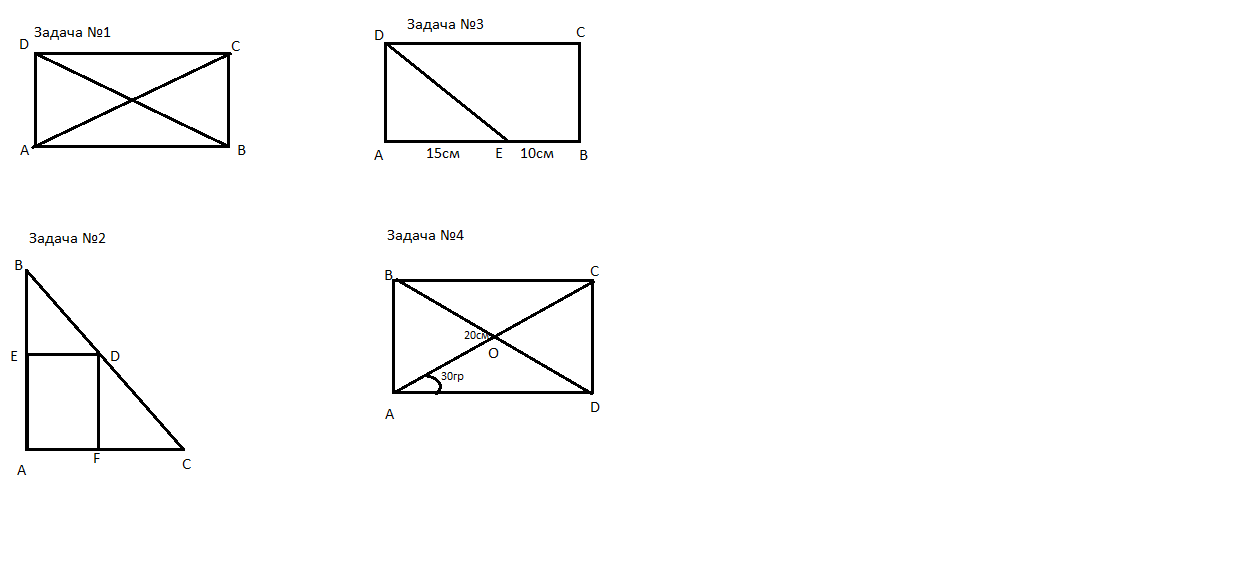
Задача №1(рисунок во вложении) Докажите,что если один из углов параллелограмма прямой,то он является прямоугольником Задача №2(рисунок во вложении) В прямоугольном равнобедренном тре-угольнике АВС с катетом 5 см из любой внутренней точки D гипотенузы АВ проведены к катетам перпендикуляры DE и DF.Найдите периметр полученного прямоугольника DECF Задача №3(рисунок во вложении) Биссектриса угла прямоугольнока делит его сторону на отрезки 19см и 15 см.Найдите периметр этого прямоугольника (рассмотреть 2 случая) Задача №4(рисунок во вложении) Диогонали прямоугольника ABCD пересекаются в точке О.Найти периметр треугольника АОВ,если угол CAD=30гр,а AC=20см Задача №5 Доказать что:параллелограмм с равными диогоналями-есть прямоугольник(рисунок 1)
Ответы
1
пусть угол А=90 - <A и <D -односторонние углы между параллельными прямыми
сумма односторонних углов 180 град D=180-90=90
в параллелограмме противолежащие углы равны <A=<C=90 ; <D=<B=90
опсс - все углы 90 град - основное свойство ПРЯМОУГОЛЬНИКА
2
не зря ведь написано прямоугольный , равнобедренный (два катета по 5 см)
у етого прямоугольника DECF - сумма двух любых смежных сторон будет равна длине катета - просто DE отсекает на катете АВ отрезки равные сторонам прямоугольника - DF -делает тоже самое
периметр прямоугольника 2*5 см =10 см
3
4
сторона AD = 20см*сos30
сторона AB = 20* sin30
периметр Р= 2*(AD+AB)= 2*20*(cos30+sin30)=2*20*(√3/2+1/2)=10(√3+1)
5
напротив диагонали АС лежит <B
напротив диагонали DB лежит <A
по теореме косинусов
AC^2=AB^2+CB^2-2*AB*BC*cosB
cosB= AC^2-(AB^2+CB^2) / 2*AB*BC (1)
BD^2=AD^2+AB^2-2*AB*AD*cosA
cosA= BD^2-(AB^2+AD^2) / 2*AD*AB =AC^2-(AB^2+CB^2) / 2*AB*BC(2)
сравним (1) и (2)
cosA=cosB
значит А=В
углы А и В односторонние и равны <A=<B=180/2=90
тоже самое рассуждение для углов D ; C
все углы 90 град -- прямоугольник