Предмет: Математика,
автор: 1Nikitin1
Доказать, что прямая  перпендикулярна к прямой
перпендикулярна к прямой 
Приложения:
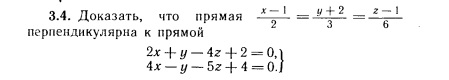
Ответы
Автор ответа:
0
Автор ответа:
0
у меня тоже вышло -72
наверное ошибка в самих условиях
наверное ошибка в самих условиях
Автор ответа:
0
спасибо
Автор ответа:
0
прямые перпендикулярны ⇔ перпендикулярны их направляющие вектора.
найдем их: прямые заданы двумя разными способами канонический и как пересечение 2-х плоскостей
а) направляющий вектор канонической прямой это знаменатели, то есть вектор (2;3;6) - направляющий вектор для прямой
б) направляющий вектор прямой заданной пересечением двух плоскостей находится, например, по формуле:
![( detleft[begin{array}{cc}B1&C1\B2&C2\end{array}right] ; detleft[begin{array}{cc}C1&A1\C2&A2\end{array}right] ; detleft[begin{array}{cc}A1&B1\A2&B2\end{array}right]) ( detleft[begin{array}{cc}B1&C1\B2&C2\end{array}right] ; detleft[begin{array}{cc}C1&A1\C2&A2\end{array}right] ; detleft[begin{array}{cc}A1&B1\A2&B2\end{array}right])](https://tex.z-dn.net/?f=%28++detleft%5Bbegin%7Barray%7D%7Bcc%7DB1%26amp%3BC1%5CB2%26amp%3BC2%5Cend%7Barray%7Dright%5D+%3B+detleft%5Bbegin%7Barray%7D%7Bcc%7DC1%26amp%3BA1%5CC2%26amp%3BA2%5Cend%7Barray%7Dright%5D+%3B+detleft%5Bbegin%7Barray%7D%7Bcc%7DA1%26amp%3BB1%5CA2%26amp%3BB2%5Cend%7Barray%7Dright%5D%29) , где А,В,С коэффициенты перед x,y,z в соответствующих уравнениях плоскостей.
, где А,В,С коэффициенты перед x,y,z в соответствующих уравнениях плоскостей.
(1*(-5)-(-1)*(-4); (-4)*4-(-5)*2;2*(-1)-1*4)=(-9;-6;-6)
для удобства следующих вычислений развернем этот вектор и разделим на 3:
(3;2;2) - направляющий вектор второй прямой
найдем скалярное произведение полученных векторов:
(2;3;6)*(3;2;2)=2*3+3*2+6*2 очевидно, что не равно нулю⇒вектора не препендикулярны друг к другу.
Таким образом данные прямые не перпендикулярны друг другу
найдем их: прямые заданы двумя разными способами канонический и как пересечение 2-х плоскостей
а) направляющий вектор канонической прямой это знаменатели, то есть вектор (2;3;6) - направляющий вектор для прямой
б) направляющий вектор прямой заданной пересечением двух плоскостей находится, например, по формуле:
(1*(-5)-(-1)*(-4); (-4)*4-(-5)*2;2*(-1)-1*4)=(-9;-6;-6)
для удобства следующих вычислений развернем этот вектор и разделим на 3:
(3;2;2) - направляющий вектор второй прямой
найдем скалярное произведение полученных векторов:
(2;3;6)*(3;2;2)=2*3+3*2+6*2 очевидно, что не равно нулю⇒вектора не препендикулярны друг к другу.
Таким образом данные прямые не перпендикулярны друг другу
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kuzserega19
Предмет: Алгебра,
автор: ksushaaaaaa40
Предмет: Биология,
автор: pgrin2017
Предмет: История,
автор: poluleh
Предмет: Геометрия,
автор: Djulhaus