Предмет: Математика,
автор: nikitaaz
Исследовать ряд на сходимость
Приложения:
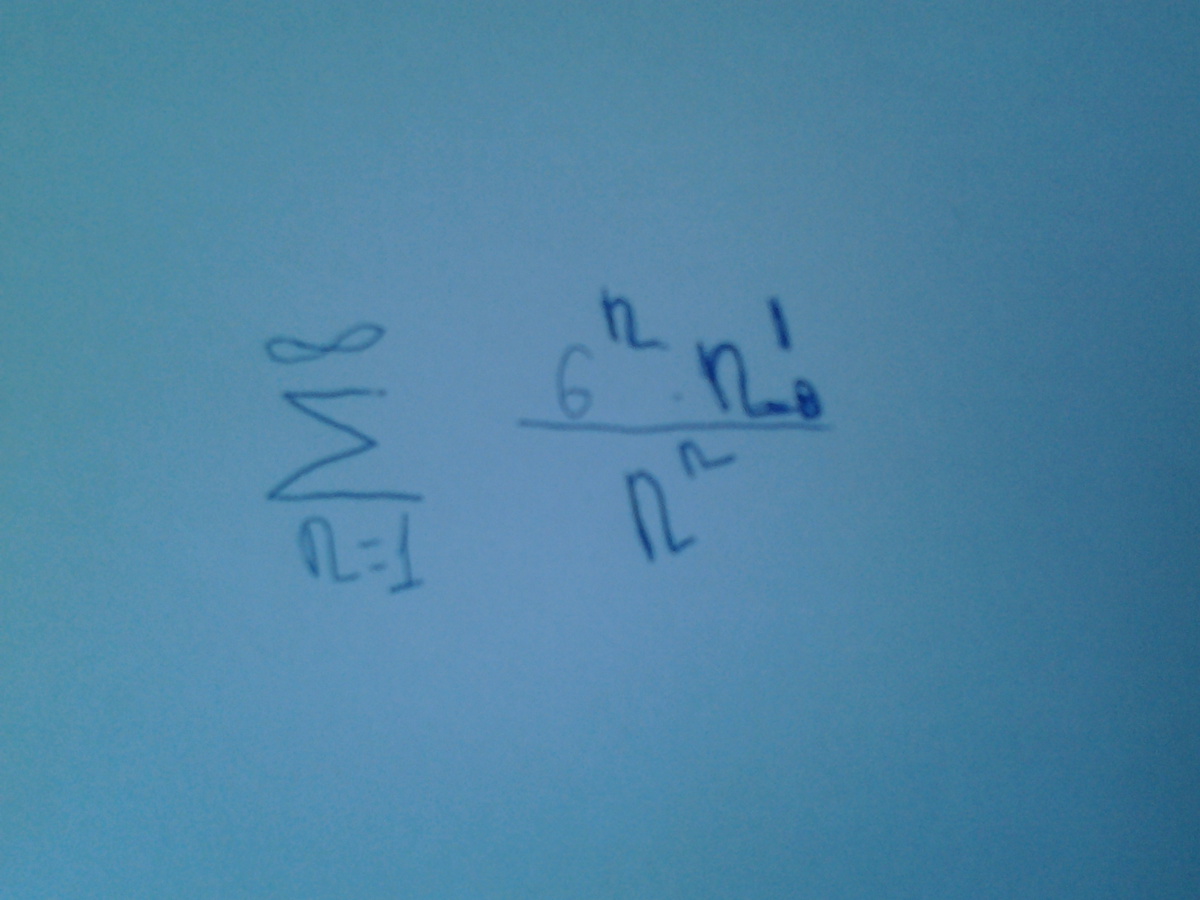
Ответы
Автор ответа:
0
По признаку Даламбера
lim(n->oo) a(n+1)/a(n) =
= lim(n->oo) [6^(n+1)*(n+1)!/(n+1)^(n+1)] : [6^n*n!/n^n] =
= lim(n->oo) [6*6^n*(n+1)*n!/((n+1)*(n+1)^n)] * [n^n/(6^n*n!)] =
= lim(n->oo) [6*6^n/6^n]*[(n+1)*n!/n!]*[n^n/((n+1)*(n+1)^n)] =
= lim(n->oo) [6*(n+1)/(n+1)]*[n/(n+1)]^n = lim(n->oo) 6*[1 - 1/(n+1)]^n =
= 6*lim(n->oo) [1 - 1/(n+1)]^(n+1-1) =
= 6*lim(n->oo) [1 - 1/(n+1)]^(n+1) : [1 - 1/(n+1)]
По Второму Замечательному пределу
lim(n->oo) [1 - 1/(n+1)]^(n+1) = e^(-1) = 1/e
Поэтому
lim(n->oo) [6^(n+1)*(n+1)!/(n+1)^(n+1)] : [6^n*n!/n^n] = 6/e
lim(n->oo) a(n+1)/a(n) =
= lim(n->oo) [6^(n+1)*(n+1)!/(n+1)^(n+1)] : [6^n*n!/n^n] =
= lim(n->oo) [6*6^n*(n+1)*n!/((n+1)*(n+1)^n)] * [n^n/(6^n*n!)] =
= lim(n->oo) [6*6^n/6^n]*[(n+1)*n!/n!]*[n^n/((n+1)*(n+1)^n)] =
= lim(n->oo) [6*(n+1)/(n+1)]*[n/(n+1)]^n = lim(n->oo) 6*[1 - 1/(n+1)]^n =
= 6*lim(n->oo) [1 - 1/(n+1)]^(n+1-1) =
= 6*lim(n->oo) [1 - 1/(n+1)]^(n+1) : [1 - 1/(n+1)]
По Второму Замечательному пределу
lim(n->oo) [1 - 1/(n+1)]^(n+1) = e^(-1) = 1/e
Поэтому
lim(n->oo) [6^(n+1)*(n+1)!/(n+1)^(n+1)] : [6^n*n!/n^n] = 6/e
Похожие вопросы
Предмет: Русский язык,
автор: aaa28042020
Предмет: Алгебра,
автор: Neznaikovskii
Предмет: Русский язык,
автор: trushkovmatvey
Предмет: Алгебра,
автор: Аноним
Предмет: Экономика,
автор: zhenyameow42305