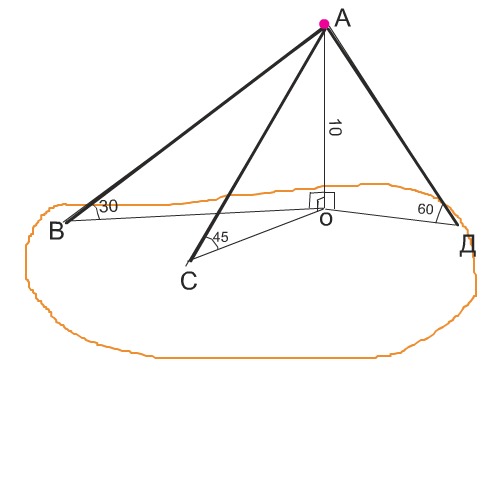
Из точки к плоскости проведены наклонные, первая с проекцией образует угол 45 градусов, вторая образует угол 60 градусов, третья 30 градусов, расстояние от точки до плоскости 10 см найти длины наклонных и проекции, сделать чертеж
Ответы
тр-к ASO: SO=10 см, угол AOS=90, SAO=45, находим гипотенузу из отношения sin 45 = √2 / 2 = SO/AS, AS=10*2/√2=20/√2; tg 45 = SO/АО=1, AO=10
тр-к BSO: SO=10 см, угол BOS=90, SBO=30, находим гипотенузу из отношения sin 30 = 1 / 2 = SO/BS, BS=10*1/2=20; tg 30 = SO/BО=√3/3, BO=30/√3
тр-к CSO: SO=10 см, угол COS=90, CAO=60, находим гипотенузу из отношения sin 60 = √3 / 2 = SO/CS, CS=10*2/√3=20/√3; tg 60 = SO/CО=√3, CO=10√3

Первая наклонная АС с проекцией ОС и перпендикуляром из А к плоскости образует равнобедренный прямоугольный треугольник АОС, где ОС=АО.
Этот треугольник - половина квадрата с диагональю АС.
По свойству диагонали квадрата
АС=10√2 см
Длина наклонной АВ вдвое больше расстояния от точки А до плоскости, т.к. это расстояние противолежит углу 30°
АВ=2·10=20 см
АД, образующую с плоскостью угол 60°, можно найти по теореме Пифагора.
ОД равно половине АД, как противолежащая углу ОАД=30°.
АД=2ОД
АД²=ОА²+ОД²
4ОД²=100+ОД²
3ОД²=100
ОД=10:√3
АД=20√3
А можно найти АД из формулы высоты равностороннего треугольника ( Ведь АОД - половина такого треугольника). Результат будет таким же.