Предмет: Геометрия,
автор: kloun12
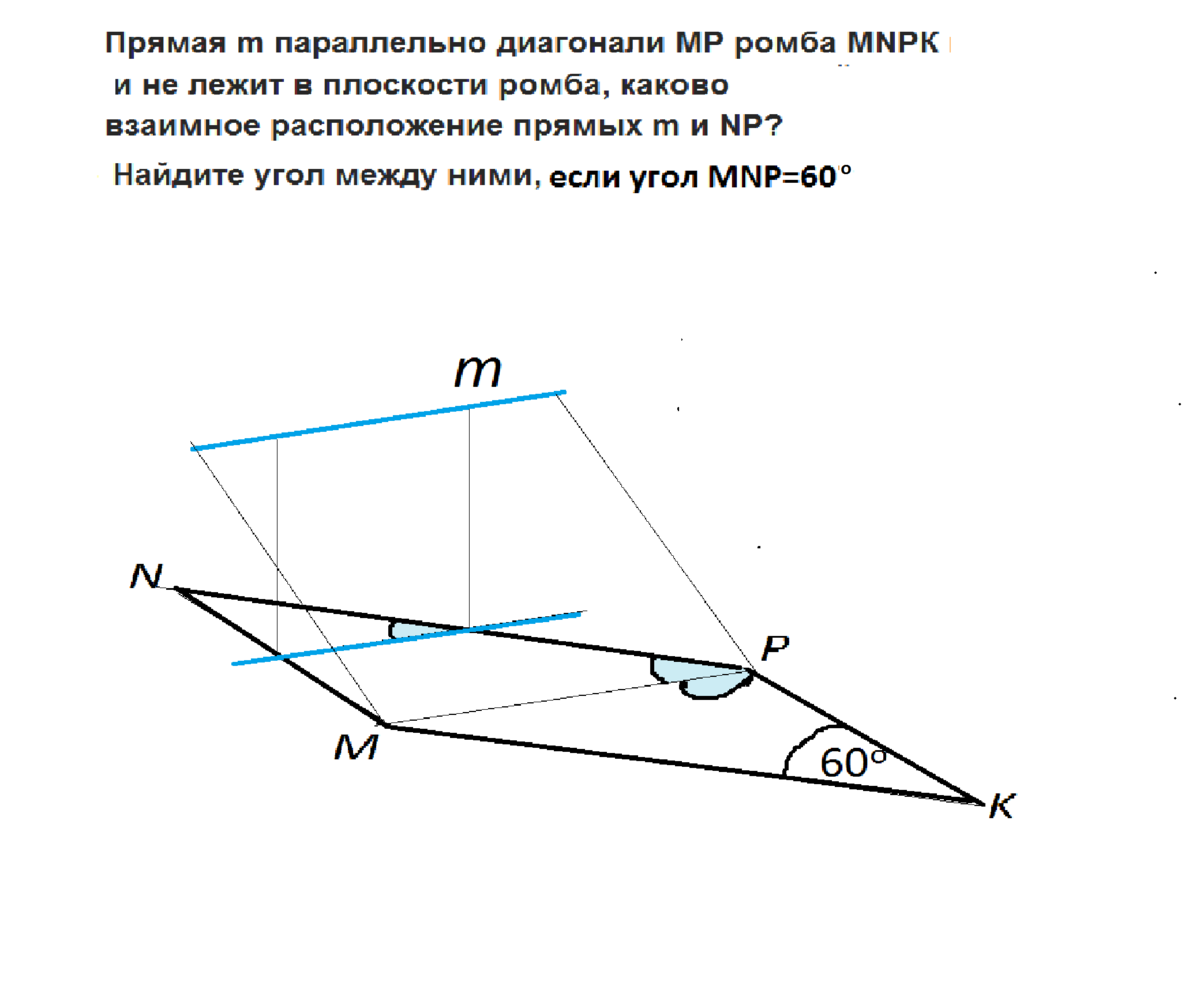
Прямая m параллельно диагонали МР ромба MNРК и не лежит в плоскости ромба, каково взаимное расположение прямых m и NP? Найдите угол между ними, угол MNP=60 градусов угол NPK=110 градусов(Полное решение прошу)
Ответы
Автор ответа:
0
Ясно что прямые скрещиваются. Тк прямая не лежит в плоскости ромба. и параллельно прямой лежащей в ней.
Понятно ,что если прямую m переместить в произвольную плоскость в пространстве, так чтобы она была параллельна прямой MP. То она будет и параллельна своему первоначальному положению. А тк ясно ,что если прямая m||m', То угол между прямой m и NP равен углу между m' и NP.
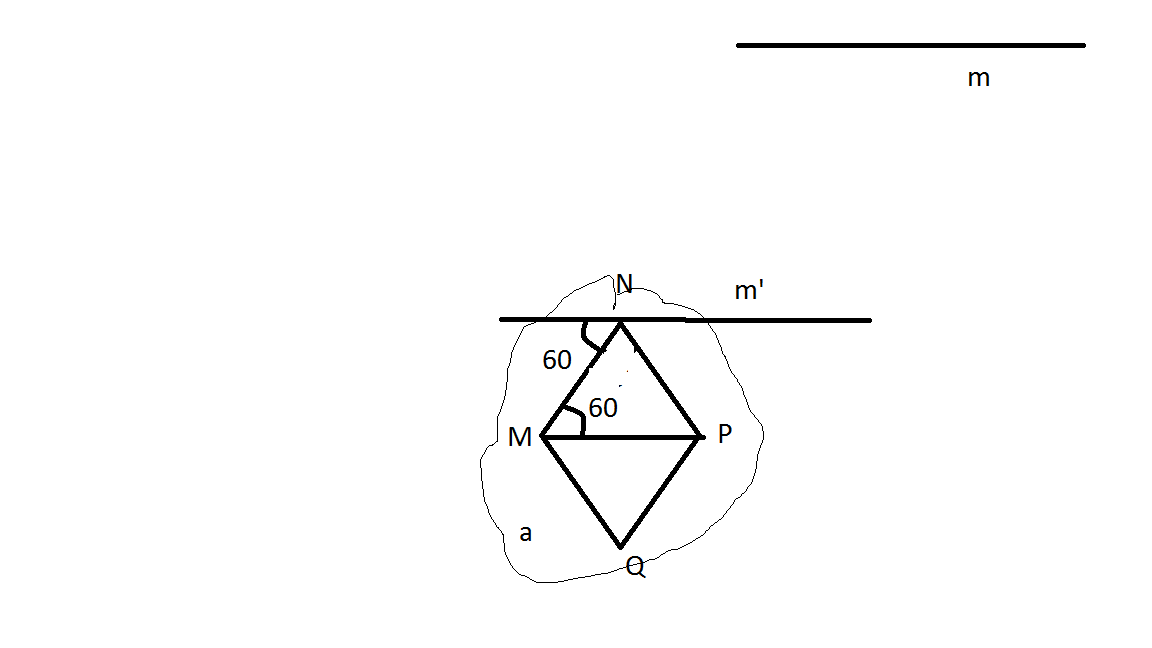
Пользуясь этим свойством, поместим вспомогательную прямую m' параллельную m
в плоскость ромба a ,так чтоб она пересекала вершину N. Смотрите рисунок.
Диагонали ромба биссектрисы его углов.
Тогда угол NMP=120/2=60.
Угол между m' и NP и данный внутренние накрест лежащие углы. Тогда угол между m' и NP 60 градусов.
Из сказанного выше выходит ,что угол между m и NP тоже равен 60
Ответ:60 ,прямые скрещиваются.
Понятно ,что если прямую m переместить в произвольную плоскость в пространстве, так чтобы она была параллельна прямой MP. То она будет и параллельна своему первоначальному положению. А тк ясно ,что если прямая m||m', То угол между прямой m и NP равен углу между m' и NP.
Пользуясь этим свойством, поместим вспомогательную прямую m' параллельную m
в плоскость ромба a ,так чтоб она пересекала вершину N. Смотрите рисунок.
Диагонали ромба биссектрисы его углов.
Тогда угол NMP=120/2=60.
Угол между m' и NP и данный внутренние накрест лежащие углы. Тогда угол между m' и NP 60 градусов.
Из сказанного выше выходит ,что угол между m и NP тоже равен 60
Ответ:60 ,прямые скрещиваются.
Приложения:
Автор ответа:
0
Использовал похожее свойство. Для решения задачи про 12 прямых. Нужно доказать что найдется угол не более 15 градусов между какими то 2 прямыми. При любом любом расположении 12 прямых на плоскости. Впрочем и для положения этих прямых в пространстве это тоже верно .
Автор ответа:
0
А хотя нет в пространстве не всегда верно :)
Автор ответа:
0
Красивая задача
Автор ответа:
0
Пока решала в блокноте. верное решение дали, но и это не будет лишним, надеюсь.
Для начала уточним, что если один угол ромба равен 60°. то второй равен 120°, а не 110°, т.к. сумма углов, прилегающих к одной стороне параллелограмма ( а ромб - параллелограмм), равна 180°.
Определение:
Две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости, не пересекаются, не параллельны и не совпадают, иначе они лежали бы в одной плоскости.
Поскольку m параллельна МР, она не параллельна NР и не лежит с ней в одной плоскости, т.к. МР и MN пересекаются.
Прямые m и NP - скрещивающиеся прямые.
Решение задачи по нахождению величины угла между скрещивающимися прямыми в принципе такое же, как при решении задачи по определению угла между пересекающимися прямыми.
То есть угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, соответственно параллельными данным.
Проекция прямой m на плоскость ромба параллельна m и параллельна МР. Она пересекается со стороной робма MN под тем же углом, под каким пересекается с этой стороной диагональ МР.
Угол между проекцией m на плоскость ромба и его стороной NP равен половине тупого угла ромба, т.к. МР, как диагональ ромба, делит угол 120 градусов пополам. (Диагонали ромба - биссектрисы его углов).
Итак, прямые m и MN скрещивающиеся и угол между ними равен 60 градусов.
Для начала уточним, что если один угол ромба равен 60°. то второй равен 120°, а не 110°, т.к. сумма углов, прилегающих к одной стороне параллелограмма ( а ромб - параллелограмм), равна 180°.
Определение:
Две прямые в трехмерном пространстве называются скрещивающимися, если они не лежат в одной плоскости, не пересекаются, не параллельны и не совпадают, иначе они лежали бы в одной плоскости.
Поскольку m параллельна МР, она не параллельна NР и не лежит с ней в одной плоскости, т.к. МР и MN пересекаются.
Прямые m и NP - скрещивающиеся прямые.
Решение задачи по нахождению величины угла между скрещивающимися прямыми в принципе такое же, как при решении задачи по определению угла между пересекающимися прямыми.
То есть угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, соответственно параллельными данным.
Проекция прямой m на плоскость ромба параллельна m и параллельна МР. Она пересекается со стороной робма MN под тем же углом, под каким пересекается с этой стороной диагональ МР.
Угол между проекцией m на плоскость ромба и его стороной NP равен половине тупого угла ромба, т.к. МР, как диагональ ромба, делит угол 120 градусов пополам. (Диагонали ромба - биссектрисы его углов).
Итак, прямые m и MN скрещивающиеся и угол между ними равен 60 градусов.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: opopopopor
Предмет: Математика,
автор: nastabojko924
Предмет: Алгебра,
автор: egavrillova1544
Предмет: Геометрия,
автор: Юллллллллллллллля
Предмет: Алгебра,
автор: verunyasvetlichnaya