Предмет: Геометрия,
автор: Vampire100
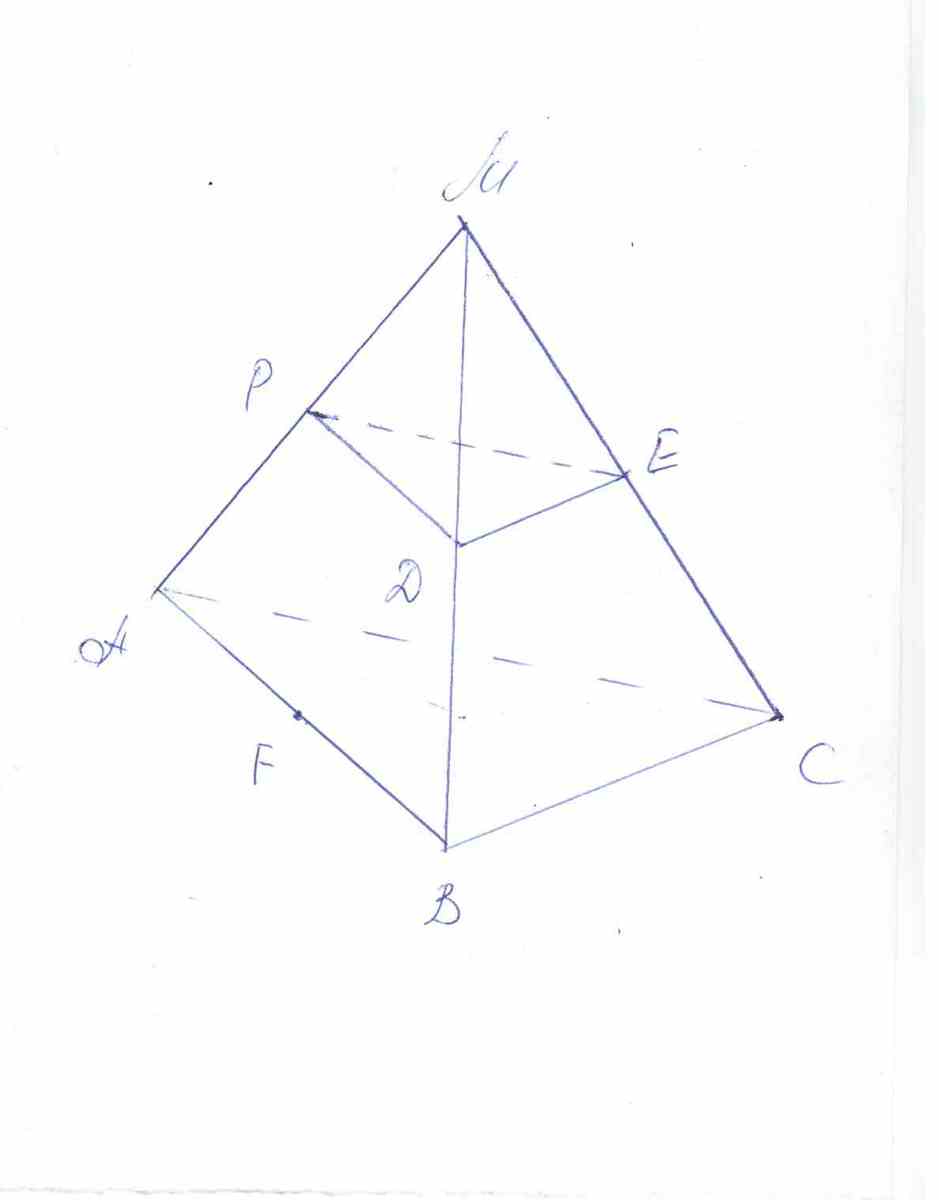
1. Дано: MABC-тетраэдр, P принадлежит AM, AC=CB=AB=AM=MB=6, D принадлежит MB, E принадлежит MC, F принадлежит AB, AF=FB. Найти площадь треугольника ABC.
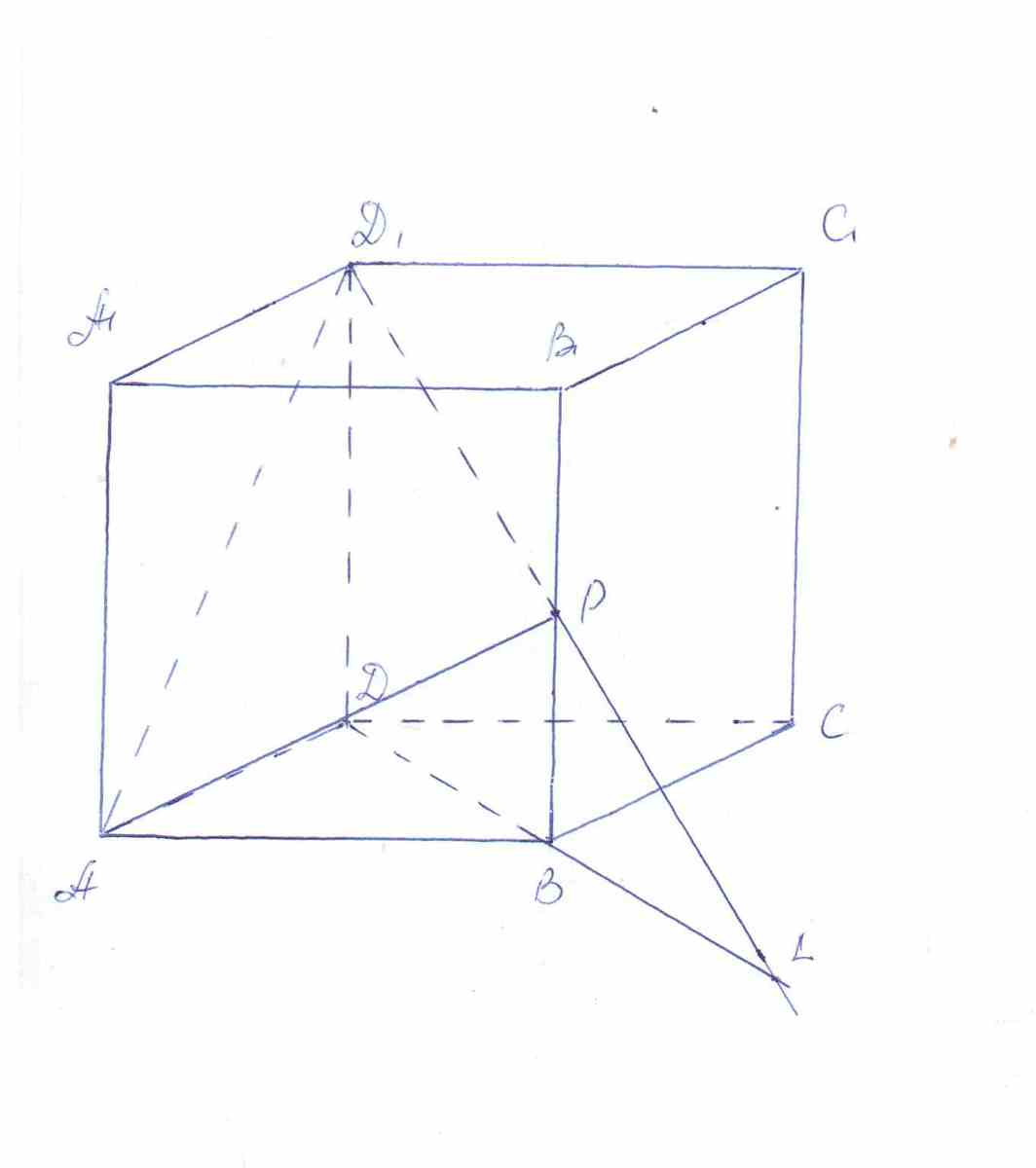
2.Дано: ABCDA1B1C1D1- куб; P принадлежит BB1; B1P=PB.
1). Построить точку пересечения D1P и плоскости ABC;
2). Как построить линию пересечения AD1P и ABB1?
3). Вычислите длину отрезков AP и A1D1, если AB=a.
Ответы
Автор ответа:
0
1.

2.3


2.3
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: Лучшиевсеглавное
Предмет: Алгебра,
автор: nazarchukmarat5
Предмет: Русский язык,
автор: sshdhfhjc
Предмет: Математика,
автор: sitnik2006
Предмет: Математика,
автор: nevoya