Предмет: Алгебра,
автор: anna1678
Срочно! Помогите пожалуйста!
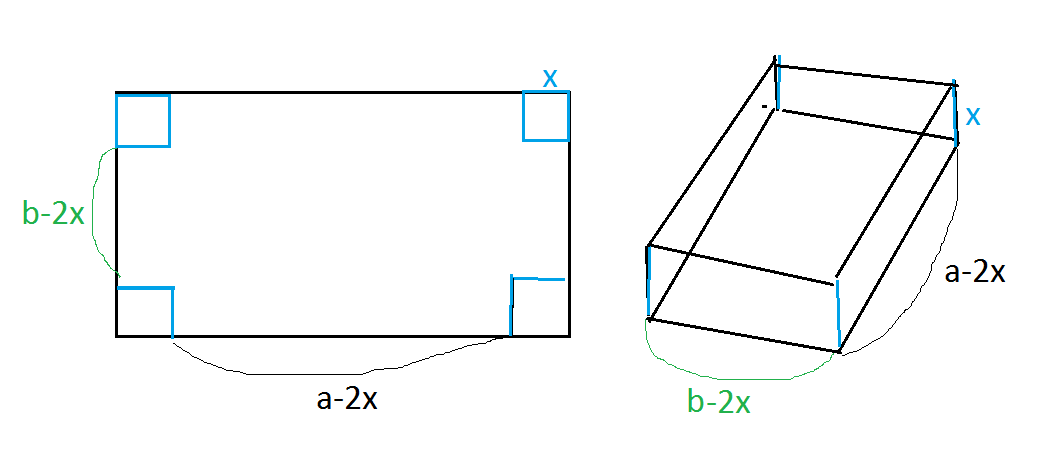
Из прямоугольного листа жести размерами axb, вырезав квадратные уголки, нужно сделать открытую коробку. Определите, какой должна быть сторона вырезанного квадрата, чтобы объем коробки был наибольшим.
Ответы
Автор ответа:
0
См. приложение
V=(a-2x)(b-2x)·x
Исследуем функцию V(x) на максимум, минимум.
Находим производную
V=4x³-2ax²-2bx²+abx
V`(x)=12x²-4ax-4bx+ab
Приравниваем к ную
12х²-4ax-4bx+ab=0
12x²-(4a+4b)x+ab=0 квадратное уравнение относительно х:
D=(4a+4b)²-4·12·ab=16a²+32ab+16b²-48ab=16a²-16ab+16b²=16(a²-ab+b²)
x₁=(4a+4b-4√(a²-ab+b²))/24 или x₂=(4a+4b+4√(a²-ab+b²))/24
Расставим знаки производной
Производная квадратичная функция, график парабола, ветви вверх
+ _ +
-----------(х₁)---------------(х₂)---------------
Наибольшее значение в т.очке х₁, так как производная меняет знак с + на _
Ответ. х=(4a+4b-4√(a²-ab+b²))/24
V=(a-2x)(b-2x)·x
Исследуем функцию V(x) на максимум, минимум.
Находим производную
V=4x³-2ax²-2bx²+abx
V`(x)=12x²-4ax-4bx+ab
Приравниваем к ную
12х²-4ax-4bx+ab=0
12x²-(4a+4b)x+ab=0 квадратное уравнение относительно х:
D=(4a+4b)²-4·12·ab=16a²+32ab+16b²-48ab=16a²-16ab+16b²=16(a²-ab+b²)
x₁=(4a+4b-4√(a²-ab+b²))/24 или x₂=(4a+4b+4√(a²-ab+b²))/24
Расставим знаки производной
Производная квадратичная функция, график парабола, ветви вверх
+ _ +
-----------(х₁)---------------(х₂)---------------
Наибольшее значение в т.очке х₁, так как производная меняет знак с + на _
Ответ. х=(4a+4b-4√(a²-ab+b²))/24
Приложения:
Автор ответа:
0
Хорошо, благодарю!
Похожие вопросы
Предмет: Українська мова,
автор: koltsovhklaagata
Предмет: География,
автор: vankov482
Предмет: Русский язык,
автор: cceloveko703
Предмет: Информатика,
автор: 434d