Question

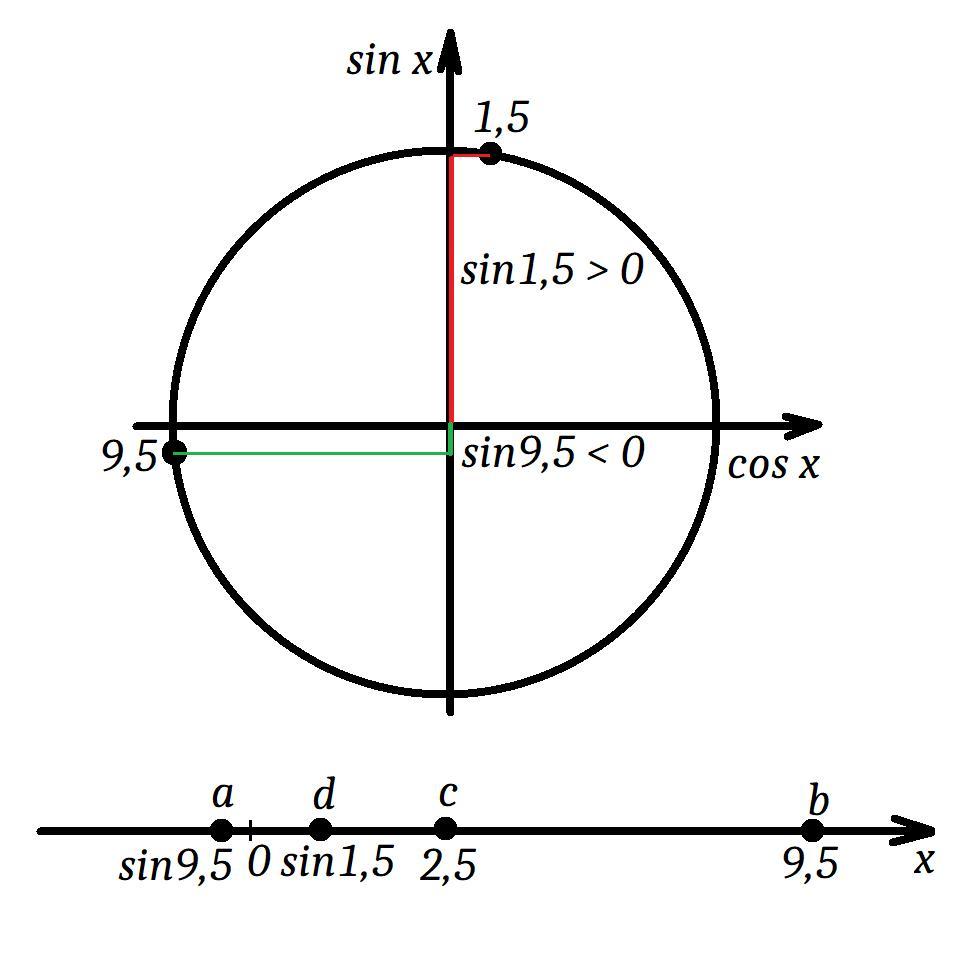
Расположит е в порядке убывания следующие числа: a=sin 9.5; b= 9.5; c= 2.5; d=sin 1.5

Answer 1

b,c,a,d   на единичной окружности, представь углы и их значения (y) и синус всегда меньше 1

Answer 2

Ответ:

Объяснение:

Дано:

a = sin 9,5

b = 9,5

c = 2,5

d = sin 1,5

__________

Расположить в порядке убывания

1)

Отбросим полный период:

a = sin (9,5) = sin (9,5 - 2π) ≈ sin (9,5 - 6,28) ≈ sin (3,22)

π ≈ 3,14

3,22 > π

Величина угла чуть больше π.

Угол лежит в III четверти.

a = Sin 3,22 - величина отрицательная, близкая к нулю.

2)

Заметим, что

1,5 < π/2 или

1,5 < 1,57...

Это I четверть.

d = sin (1,5) величина положительная, близкая к 1.

В порядке убывания:

b → c → d → a

Answer 3

Множества значений синуса: [-1;1], поэтому наибольшим число будет b=9,5 далее будет c=2,5.

Сравним a и d:

На тригонометрической окружности π это половина круга, а  синус угла это его проекция на ось ординат;

π ≈ 3,14  ⇒  $displaystyle frac{pi}2 approx frac{3,! 14}2 =1,! 57$

На самом деле π чуть больше 3,14 поэтому $displaystyle frac{pi}2 >1,! 57>1,!5 Rightarrow frac{pi}2 >1,! 5$ , то есть 1,5 лежит в 1 четверти ближе к границе со 2 четвертью.

Определим примерное положение 9,5.

9,5 - 3·3,14 = 0,50-0,42 = 0,08

π = 3,141... Поэтому 9,5-3·π > 0,08-(3·0,002) = 0,074

Таким образом на окружности 9,5 ∈ (π+0,074 ; π+0,08), то есть лежит в 3 четверти, ближе к границе со 2 четвертью.

Сравнение синусов смотри в приложении.

Ответ: b, c, d и a.