Предмет: Математика,
автор: nfb137
Помогите пожалуйста, как это решить!?(написать подробно)
cos(0.5arctg(8/15)-0.5pi)=?
Ответы
Автор ответа:
0
cos(0.5arctg(8/15)-0.5pi) - ?
arctg(8/15) = x угол
tg(arctg(8/15)) = 8/15
значит:
a = 8 катет
b = 15 катет
c = √(8²+15²) = √(64+225) = √289 = 17 гипотенуза
х = arctg(8/15) угол между b и c
cos(0.5x-pi/2) = sin(0.5x) =>
=> cos(0.5arctg(8/15)-0.5pi) = sin(0.5arctg(8/15))
sin(x) = sin(arctg(8/15)) = 8/17
cos(x) = cos(arctg(8/15)) = 15/17
Формулa половинного аргумента:
sin²(x/2) = (1 - cosx)/2
sin²(x/2) = (1 - 15/17)/2
sin²(x/2) = 1/17
sin(x/2) = ±1/√17 = ±√17/17
sin(x/2) = sin(0.5arctg(8/15)) = cos(0.5arctg(8/15)-0.5pi) =1/√17 = √17/17
cos(0.5arctg(8/15)-0.5pi) = 1/√17 = √17/17
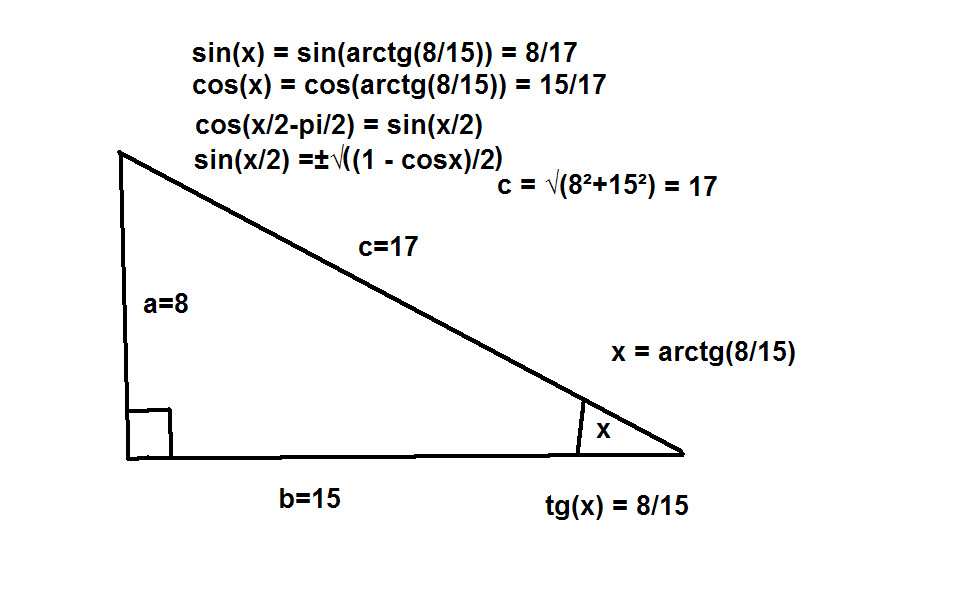
РИСУНОК НИЖЕ:
arctg(8/15) = x угол
tg(arctg(8/15)) = 8/15
значит:
a = 8 катет
b = 15 катет
c = √(8²+15²) = √(64+225) = √289 = 17 гипотенуза
х = arctg(8/15) угол между b и c
cos(0.5x-pi/2) = sin(0.5x) =>
=> cos(0.5arctg(8/15)-0.5pi) = sin(0.5arctg(8/15))
sin(x) = sin(arctg(8/15)) = 8/17
cos(x) = cos(arctg(8/15)) = 15/17
Формулa половинного аргумента:
sin²(x/2) = (1 - cosx)/2
sin²(x/2) = (1 - 15/17)/2
sin²(x/2) = 1/17
sin(x/2) = ±1/√17 = ±√17/17
sin(x/2) = sin(0.5arctg(8/15)) = cos(0.5arctg(8/15)-0.5pi) =1/√17 = √17/17
cos(0.5arctg(8/15)-0.5pi) = 1/√17 = √17/17
РИСУНОК НИЖЕ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: fasshoin
Предмет: Геометрия,
автор: Mihutkaaa
Предмет: Математика,
автор: karyrobloxian
Предмет: Математика,
автор: Vikusiy1001
Предмет: Алгебра,
автор: dimkaa12