Question

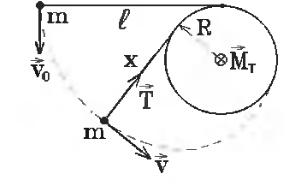
На поверхности стола расположен вертикальный цилиндр радиуса R . К некоторой точке цилиндра прикреплена невесомая нерастяжимая нить длиной l0 , к концу которой привязано тело. Телу сообщают скорость v ,
направленную перпендикулярно нити так, что нить начинает наматываться на
цилиндр. Найти время, за которое нить полностью намотается на цилиндр. Трение отсутствует.

Ответ:lo^2/2Rv

Прошу рассказать как решить)

Answer 1

Задача нелегкая.

Пусть в некоторый момент времени длина свободного конца нити равна х. Скорость грузика v остается перпендикулярной нити(в противном случае грузик бы ослаблял нить, либо разрывал). Поэтому сиа натяжения нити Т перпендикулярна к траектории грузика, работу не производит, а величина скорости грузика сохраняется

$v=v_0=const$.

Под действием момента силы натяжения относительно оси цилиндра $M_T=RT$ уменьшается момент импульса грузика $L=mvx$

$frac{dL}{dt}=-M_T$ или $mvfrac{dx}{dt}=-RT$

d-дельта.

Подставими в это соотношение величину силы натяжения из уравнения движения $T=ma_n=frac{mv^2}{x}$, получим уравнение $frac{dx}{dt}=-frac{Rv}{x}$. Разделяем в нем переменные и интегрируем обе части с учетом начальных условий задачи:

$intlimits^0_l {x} , dx=-Rv_0intlimits^t_0 {} , dt$

$frac{x^2}{2}|^0_l=-Rv*(t)|^t_0$

$0-frac{l^2}{2}=-Rv*t$

$t=frac{l^2}{2Rv}$

откуда время движения грузика равно $t=frac{l^2}{2Rv}$