Question

диагонали четырехугольника  ABCD, пересекаются под прямым углом,делятся пополам. Длины диагоналей равны 6 см и 8 см. Как вычислить площадь четырехугольника АВСD

Answer 1

Ответ:

24 см²

Пошаговое объяснение:

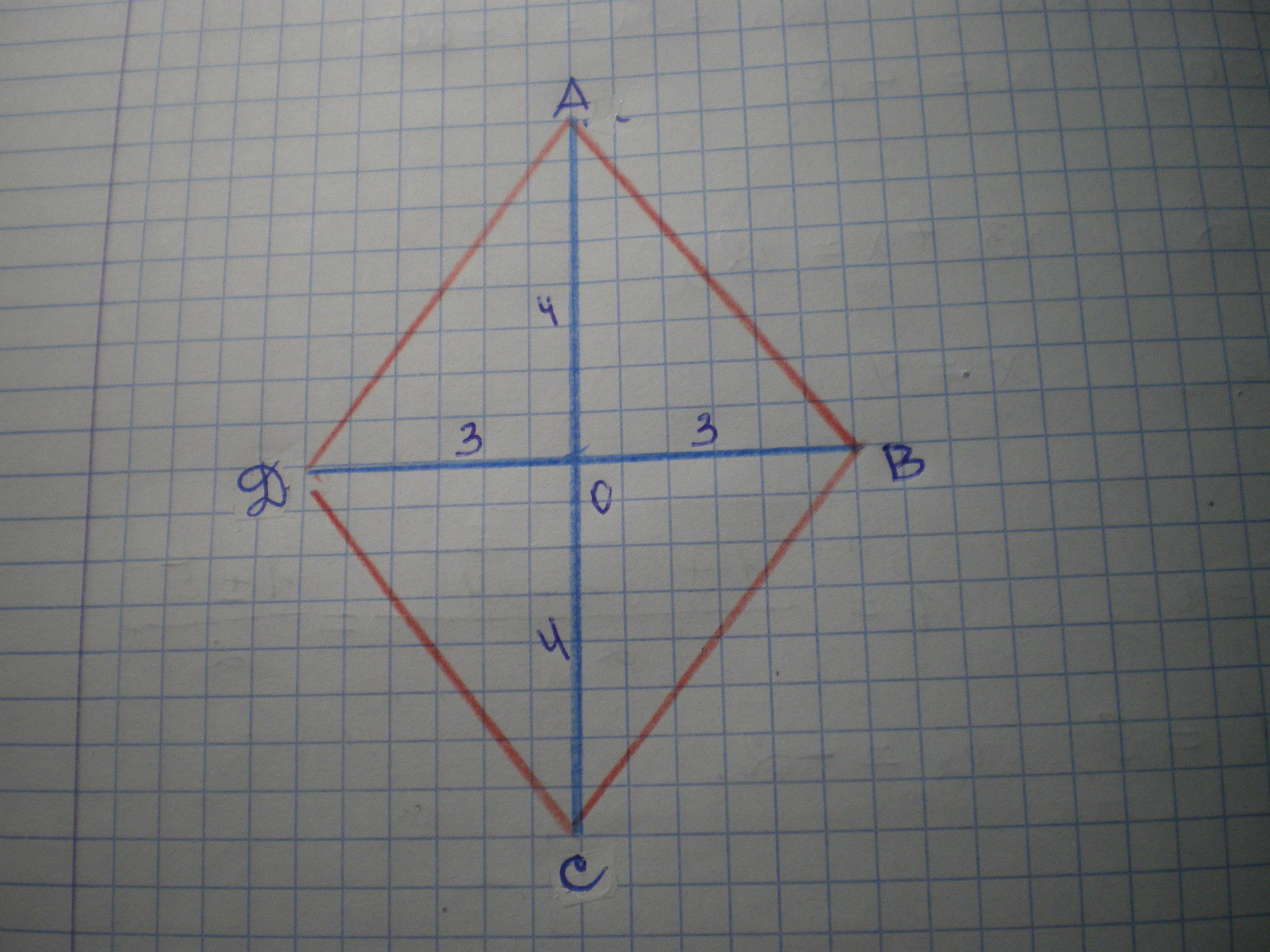
Четырехугольник  ABCD - ромб, т.к. диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.

АО=ОС=8:2=4 см

DО=ОВ=6:2=3 см.

ΔАОD=ΔDOC=ΔCOB=ΔAOB.

Найдем площадь любого из этих треугольников и умножим её на 4.

S(АОВ)=1/2 * АО * ОВ=1/2 * 3 * 4 = 6 см²

S(ABCD)=6*4=24 см²