Question

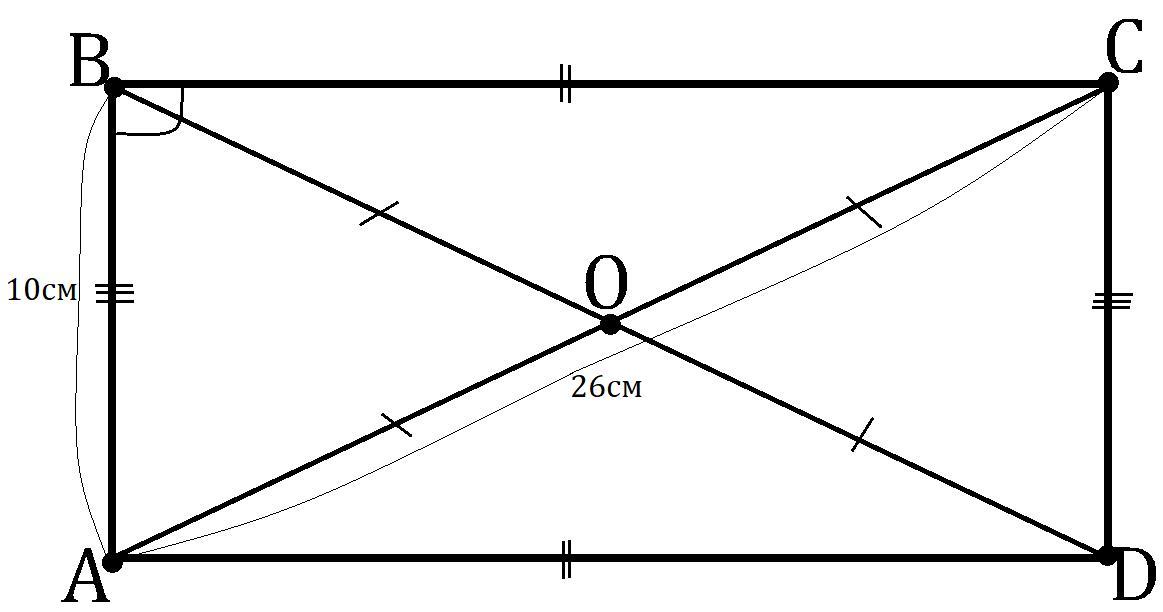
В прямоугольнике ABCD диагонали пересекаются в точке о, AB=10,AC=26см.Найдите а)BC б)AB+OD в)DA-1/2 CA

Answer 1

Дано: ABCD - прямоугольник; AB=10см; AC=26см; AC∩BD=O.

В прямоугольника диагонали равны и делятся точкой пересечения пополам ⇒ AO=OC=BO=OD. Противоположные стороны равны ⇒ AB=CD; BC=DA. И углы между сторонами равны 90°.

а) ΔABC - прямоугольный, найдём по теореме Пифагора неизвестный катет  ΔABC.

AC² = AB²+BC² ⇒ BC² = AC²-AB²; $BC=sqrt{AC^2-AB^2}=$

$=sqrt{26^2-10^2}=sqrt{2^2cdot (169-25)}=2cdot 12=24$ см

б) OD = DB÷2 = AC÷2 = 26см÷2 = 13см.

AB+OD = 10см+13см = 23см.

в) DA = BC = 24см.

DA-CA÷2 = 24см-26см÷2 = 24см-13см = 11 см.

Ответ: a) 24см; б) 23см; в) 11см.