Предмет: Алгебра,
автор: love67
вычислить пределы сколько сможете))))
Забыла,как делать) напомнить)
Приложения:
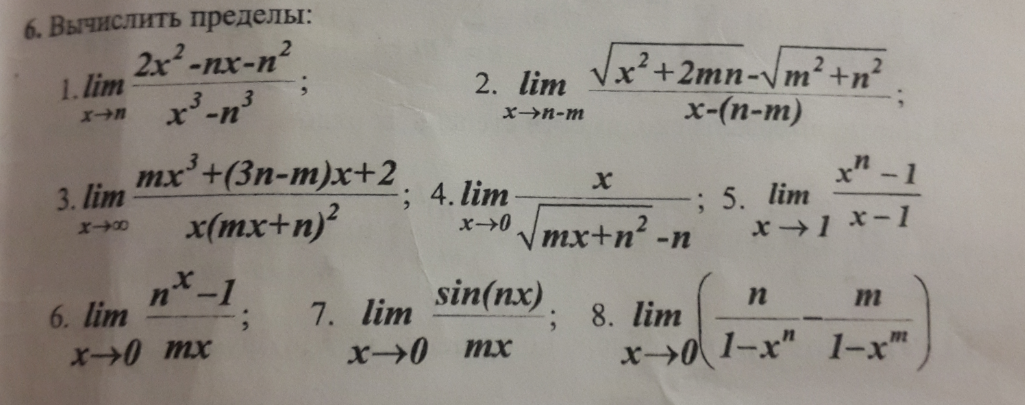
Ответы
Автор ответа:
0
Автор ответа:
0
В №5 пользуемся разложением:

В №№6 и 7 заменяем бесконечно малые величины на эквивалентные.
В №№6 и 7 заменяем бесконечно малые величины на эквивалентные.
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: sonyat1308
Предмет: История,
автор: lizacozlovec
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: 89196343729
Предмет: Геометрия,
автор: KonechnaNika