Предмет: Геометрия,
автор: INastaska
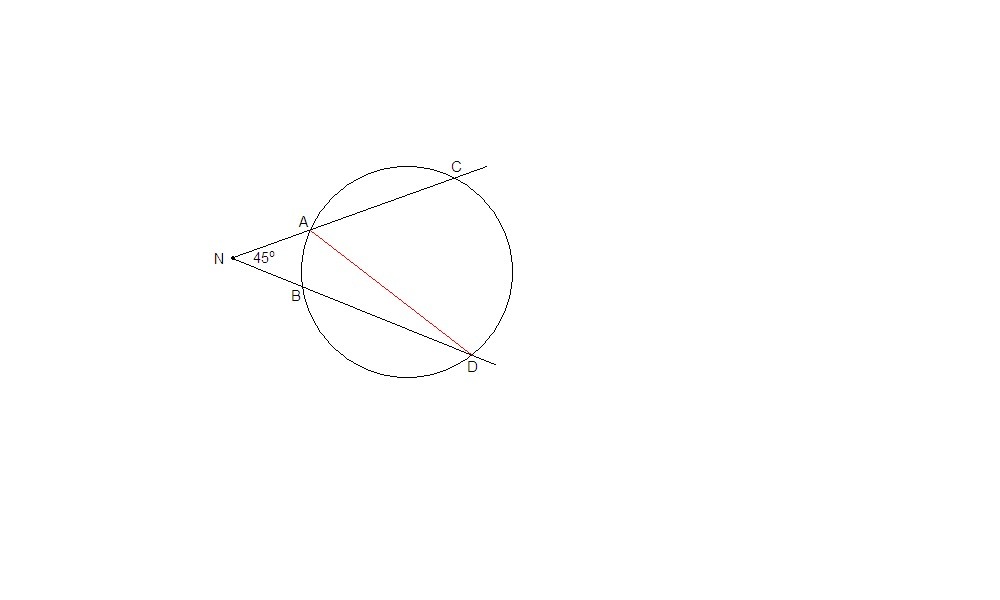
Из точки N, лежащей вне окружности, проведены к ней две секущие, образующие угол 45°. Меньшая дуга окружности, заключенная между сторонами угла, равна 30°. Найти величину большей дуги.
Ответы
Автор ответа:
0
Проведем хорду AD.
∠ADB вписанный, опирается на дугу в 30°, значит
∠ADB = 15°
∠CAD - внешний угол треугольника NAD и равен сумме двух внутренних углов, не смежных с ним:
∠CAD = ∠AND + ∠ADN = 45° + 15° = 60°
Угол CAD вписанный, опирается на дугу CD, значит дуга в два раза больше:
∪СD = 60° · 2 = 120°
Стоит запомнить: угол между секущими равен половине разности высекаемых дуг.
∠ADB вписанный, опирается на дугу в 30°, значит
∠ADB = 15°
∠CAD - внешний угол треугольника NAD и равен сумме двух внутренних углов, не смежных с ним:
∠CAD = ∠AND + ∠ADN = 45° + 15° = 60°
Угол CAD вписанный, опирается на дугу CD, значит дуга в два раза больше:
∪СD = 60° · 2 = 120°
Стоит запомнить: угол между секущими равен половине разности высекаемых дуг.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: likamil10880
Предмет: Русский язык,
автор: vikaaa68
Предмет: История,
автор: kseniyarassk2008
Предмет: Литература,
автор: немешка