Question

исследуйте функцию f(x)=4x^4-16/3*x^3
Укажите множество значений данной функции
сколько корней имеет уравнение?

Answer 1

Иссоледуем функцию $f(x)=4x^4- frac{16}{3x^3}$
1) Область определения.
Знаменатель не должен равен нулю
$x neq 0 \ D(f)=(-infty;0)cup(0;+infty)$
2) Первая производная функции:
$f'(x)=(4x^4)'-( frac{16}{3x^3} )'=16x^3+ frac{16}{x^4}$
3) Вторая производная
$f''(x)=(16x^3)'+( frac{16}{x^4} )'=48x^2- frac{64}{x^5}$
4) критические точки (первая производная равна нулю)
$16x^3+ frac{16}{x^4} =0|cdot x^4 \ 16x^7+16=0 \ 16(x^7+1)=0 \ x^7+1=0 \ x=-1$
5) Точки перегиба (Вторая производная равна нулю
$48x^2- frac{64}{x^5} =0|cdot x^5 \ 48x^7-64=0\3x^7=4 \ x^7= frac{4}{3} \ \ x= frac{ sqrt[7]{2916} }{3}$
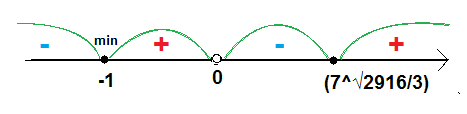
Проходя через точку минимума, производная функции меняет знак с - на +.
Относительный минимум - ($(-1; frac{28}{3} )$