Предмет: Геометрия,
автор: Zumarto
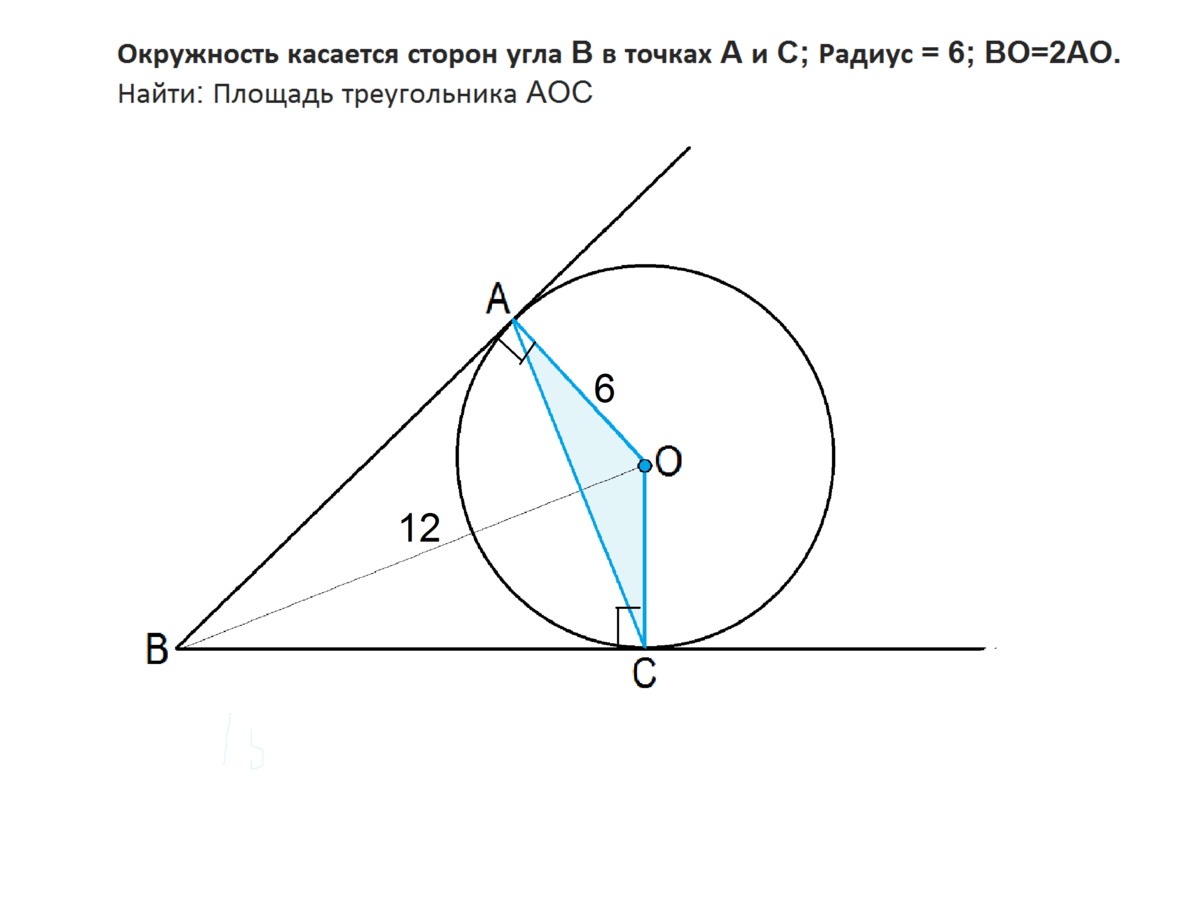
Окружность касается сторон угла B в точках A и C; Радиус = 6; BO=2AO.
Найти: Площадь треугольника AOC
Ответы
Автор ответа:
0
Проведем радиусы АО и ОС к точкам касания.
В прямоугольном треугольнике ВАО катет, противолежащий углу АВО, равен половине гипотенузы ВО.
sin ABO=6:12=0,5, и это синус угла 30°
ВА=ВС как отрезки касательных из одной точки к окружности.
Треугольники АВО и ВОС равны по трем сторонам.
Угол АОВ=2×угол ВОА=2·(90°-30°)=120°
Площадь треугольника АОС равна половине произведения АО·ОС·sin АОС sin АОС=sin 120°=(√ 3):2
S Δ(АОС)=0,5·6² ·(√ 3):2=9√3
В прямоугольном треугольнике ВАО катет, противолежащий углу АВО, равен половине гипотенузы ВО.
sin ABO=6:12=0,5, и это синус угла 30°
ВА=ВС как отрезки касательных из одной точки к окружности.
Треугольники АВО и ВОС равны по трем сторонам.
Угол АОВ=2×угол ВОА=2·(90°-30°)=120°
Площадь треугольника АОС равна половине произведения АО·ОС·sin АОС sin АОС=sin 120°=(√ 3):2
S Δ(АОС)=0,5·6² ·(√ 3):2=9√3
Приложения:
Автор ответа:
0
Спасибо огромное! Снова выручили :)
Похожие вопросы
Предмет: Геометрия,
автор: dimonlimon2k19
Предмет: Алгебра,
автор: nikto111213
Предмет: Русский язык,
автор: AmuckPVP
Предмет: Физика,
автор: Аноним
Предмет: Биология,
автор: максимр