Question

Помогите сделать два задание пожалуйста
Только под цифрой 10

Answer 1

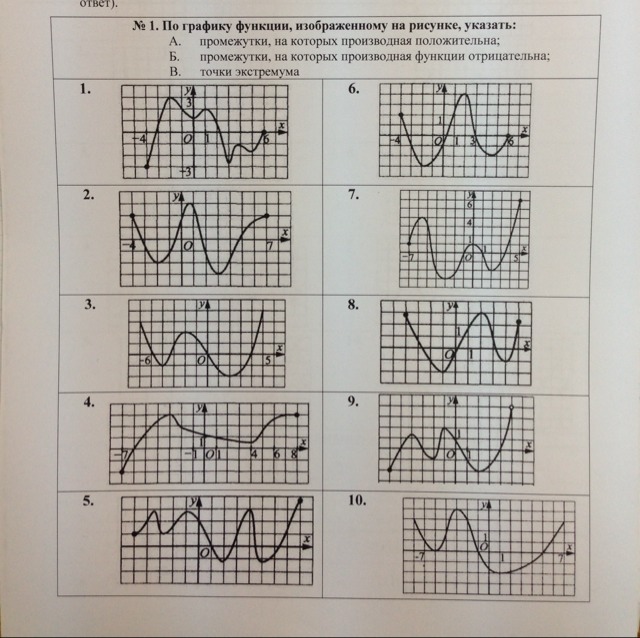
Номер 10.(картинка 1)
1) возрастает на промежутке [-6;-4]U[1;+бесконечность)
2) убывает на промежутке (-беск;-7]U[-4;1]
3) Точки экстремумы - производная равна нулю (х=-6; x=-1 и x=5)
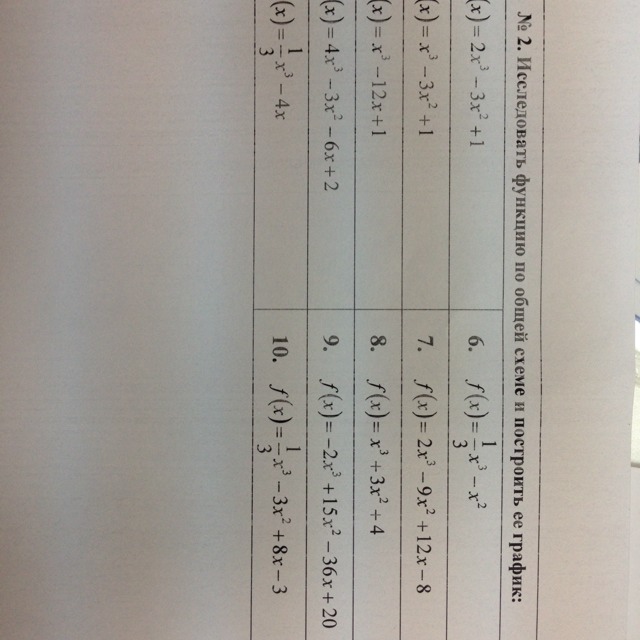
Номер 10. (картинка 2)
$f(x)= frac{1}{3} x^3-3x^2+8x-3$
1) Область определения функции: множество всех действительных чисел.
2) первая Производная.
$f'(x)=x^2-6x+8$
3) производная равна нулю
$f'(x)=0 \ x^2-6x+8=0$
 Находим дискриминант
$D=b^2-4ac=(-6)^2-4cdot1cdot8=4$
Дискриминант больше нуля, значит уравнение имеет 2 корня
$x_1_,_2= dfrac{-bpm sqrt{D} }{2a} \ \ x_1=2 \ x_2=4$
4) Вторая производная 
$f''(x)=(x^2-6x+8)'=2x-6$
5) Точки перегиба.Вторая производная равна нулю
$2x-6=0 \ x=3$ точка перегиба

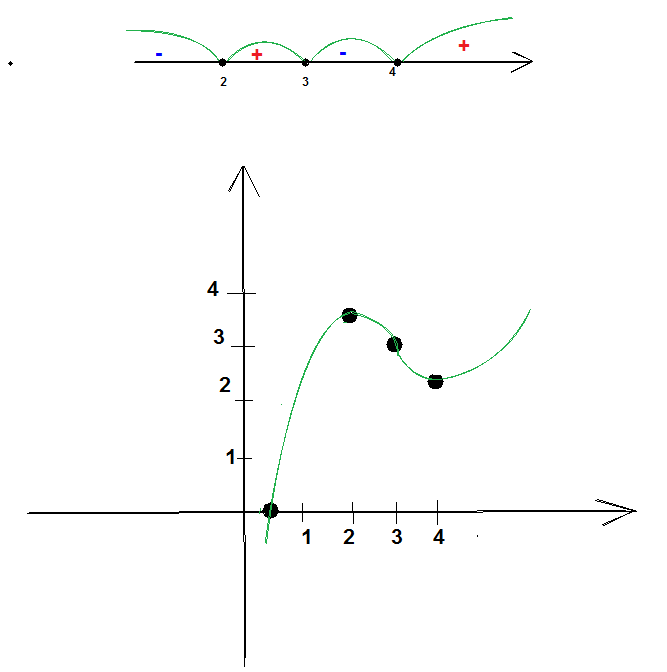
Теперь осталось нарисовать) смотрите во вложении