Question

Построить треугольник ABC по гипотенузе AB и медиане AA1. Помогите, пожалуйста, ОЧЕНЬ НАДО

Answer 1

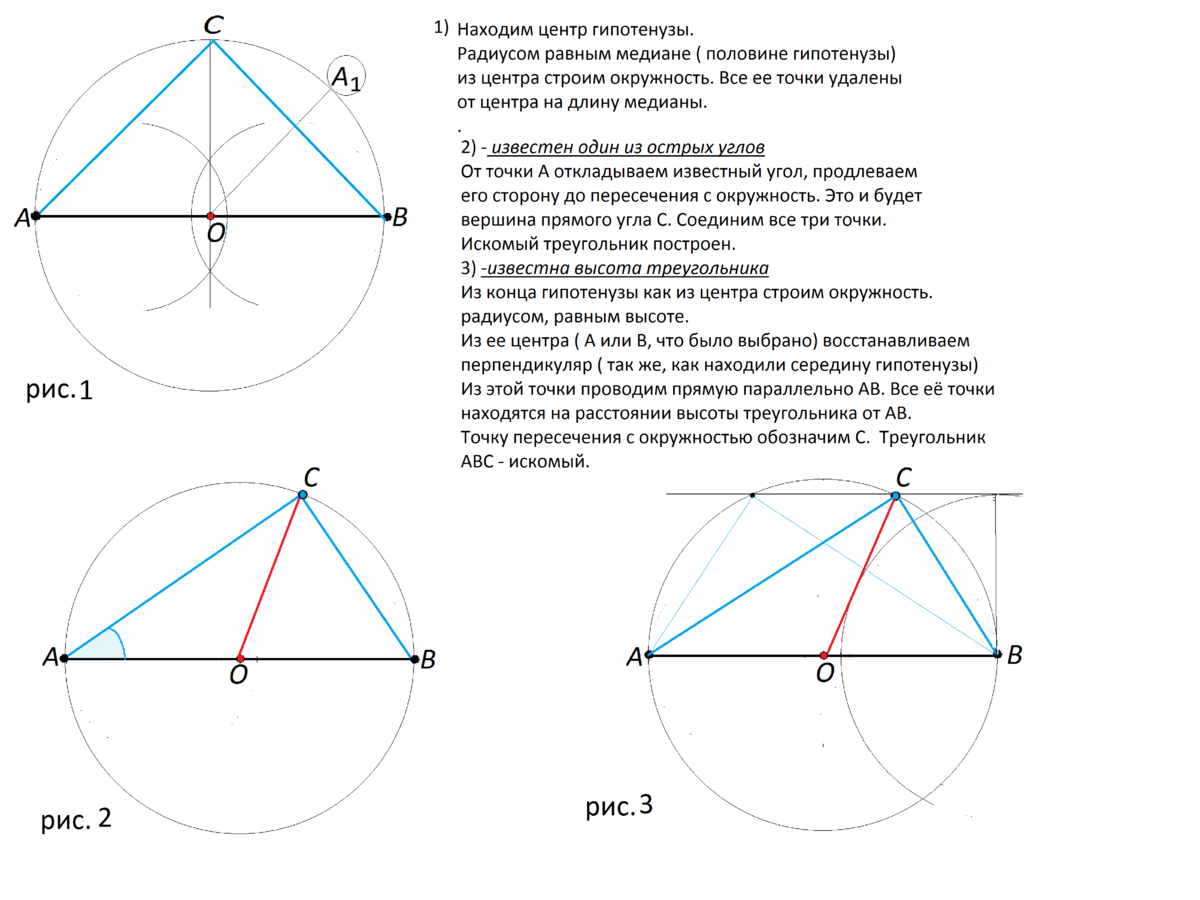
 Для построения  треугольника недостаточно данных; нужны еще один из острых углов или высота треугольника.
Как известно, длина медианы прямоугольного треугольника равна половине длины его гипотенузы и равна длине радиуса, описанного вокруг этого треугольника.
Начертим гипотенузу АВ. По известной методике деления отрезка на две равные части находим ее середину О.
Для этого из концов А и В чертим полуокружности радиусом больше половины отрезка, точки их пересечения соединяем прямой.
Эта прямая  делит АВ пополам и является перпендикуляром к АВ.
Место пересечения обозначим О ( ОА=АА1, как дано в задаче)
Вариант 1.
 Соединяем О с точкой пересечения перпендикуляра и окружности. Это вершина С. Соединяем А, В, С.  Получен равнобедренный прямоугольный треугольник АВС.
Вариант 2.
Из А, как из вершины откладываем известные острый угол, проводим его сторону до пересечения с окружностью.  Точка пересечения - вершина угла С.  АВС - искомый треугольник.
Вариант 3.
Из А или В возводим перпендикуляр, равный заданной длине высоты треугольника. Проводим параллельно АВ прямую. Все ее точки равноудалены от АВ.
Точку пересечения прямой и окружности обозначим С.
Треугольник АВС - искомый. 

Answer 2

Данных достаточно. И медиана проведена из точки А, так же как и гипотенуза имеет обозначение АB

Answer 3

Не совсем. С этими данными как углы треугольника, так и его высота могут иметь любые значения. Только днины гипотенузы и медианы будут одни и те же.