Предмет: Математика,
автор: ТипУмная
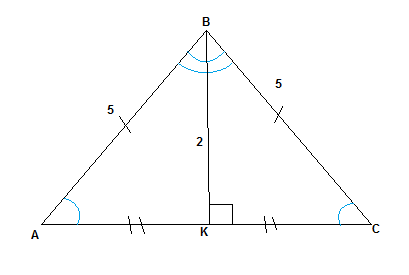
Найдите площадь равнобедренного треугольника по боковой стороне и высоте, опущенной на основание, которые равны соотвественно 5 см и 2 см
Ответы
Автор ответа:
0
У равнобедренного треугольника боковые стороны и углы при основания равны. АВ = ВС, угол А = углу С. Высота ВК проведенная к стороне основания АС делит основания пополам. АК = СК = АС/2.
С прямоугольного треугольника АВК (угол АКВ = 90 градусов)
По т. Пифагора(квадрат гипотенузы равна сумме квадратов катетов)

Тогда сторона основания в 2 раза больше АК,
Площадь равнобедренного треугольника равна полупроизведению основанию АС на высоту, проведенной к этой стороне

Ответ: 2√21 см²
С прямоугольного треугольника АВК (угол АКВ = 90 градусов)
По т. Пифагора(квадрат гипотенузы равна сумме квадратов катетов)
Тогда сторона основания в 2 раза больше АК,
Площадь равнобедренного треугольника равна полупроизведению основанию АС на высоту, проведенной к этой стороне
Ответ: 2√21 см²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: cookiepechenkovich
Предмет: Математика,
автор: kydyralievaipery2009
Предмет: Математика,
автор: liliyaovsepyan123
Предмет: Физика,
автор: Аноним
Предмет: Физика,
автор: YOUNG708