Предмет: Геометрия,
автор: vika090998
Доказать что параллелограмм является ромбом, если его сторона образует с диагоналями углы, сумма которых равно 90(градусов)
Ответы
Автор ответа:
0
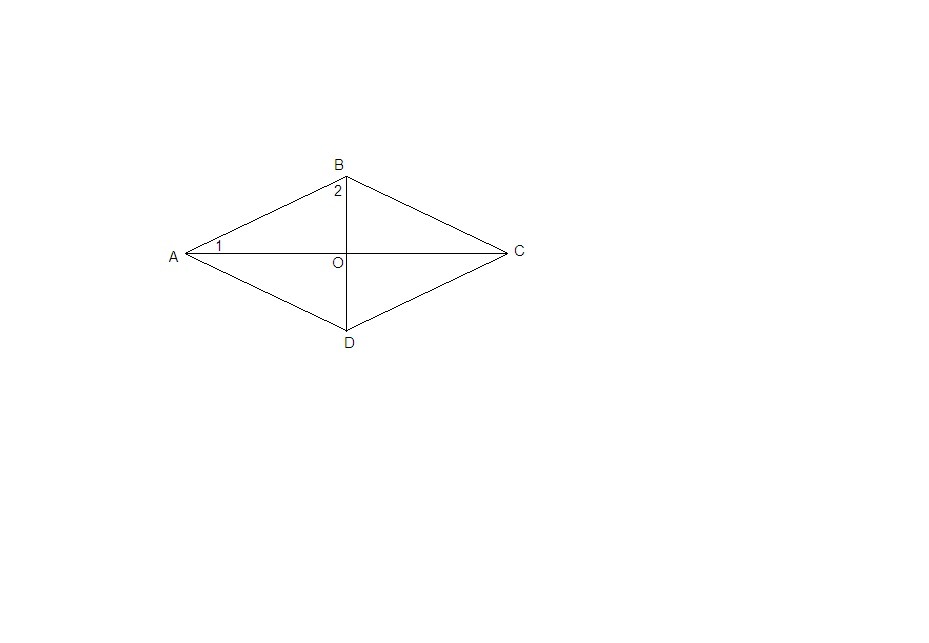
Обозначим угол между стороной АВ и диагональю АС ∠1,
а угол между стороной АВ и диагональю BD ∠2.
По условию ∠1 + ∠2 = 90°.
Тогда в ΔАОВ ∠АОВ = 180° - (∠1 + ∠2) = 180° - 90° = 90°.
Т.е. АС ⊥ BD.
А если в параллелограмме диагонали перпендикулярны, то это ромб.
а угол между стороной АВ и диагональю BD ∠2.
По условию ∠1 + ∠2 = 90°.
Тогда в ΔАОВ ∠АОВ = 180° - (∠1 + ∠2) = 180° - 90° = 90°.
Т.е. АС ⊥ BD.
А если в параллелограмме диагонали перпендикулярны, то это ромб.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: turegeldiadela0911
Предмет: Литература,
автор: ychenica54
Предмет: Қазақ тiлi,
автор: z84966947
Предмет: Информатика,
автор: 228л