Предмет: Геометрия,
автор: Zenattu
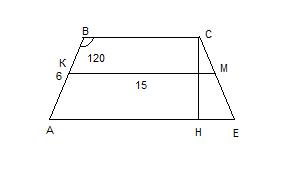
Боковая сторона равнобедренной трапеции равна 6 см, один из её углов равен 120 градусов, а средняя линия трапеции равна 15 см. Найдите площадь трапеции.
Ответы
Автор ответа:
0
В равнобедренной трапеции углы В и С равны по 120°. Найдем углы при основании АЕ:
<A=<E=(360-120*2):2=60°
Построим высоту СН. В прямоугольном треуг-ке СНЕ найдем катет СН:
sin E=CH:CE, отсюда CH=sin E*CE=sin 60 * 6=√3/2*6=3√3 см
Находим площадь трапеции, зная, что она равна произведению полусуммы ее оснований на высоту, т.е. произведению средней линии на высоту:
S=KM*CH=15*3√3=45√3 см²
<A=<E=(360-120*2):2=60°
Построим высоту СН. В прямоугольном треуг-ке СНЕ найдем катет СН:
sin E=CH:CE, отсюда CH=sin E*CE=sin 60 * 6=√3/2*6=3√3 см
Находим площадь трапеции, зная, что она равна произведению полусуммы ее оснований на высоту, т.е. произведению средней линии на высоту:
S=KM*CH=15*3√3=45√3 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: sofik53
Предмет: МХК,
автор: Аноним
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: sandra8