Предмет: Геометрия,
автор: Аноним
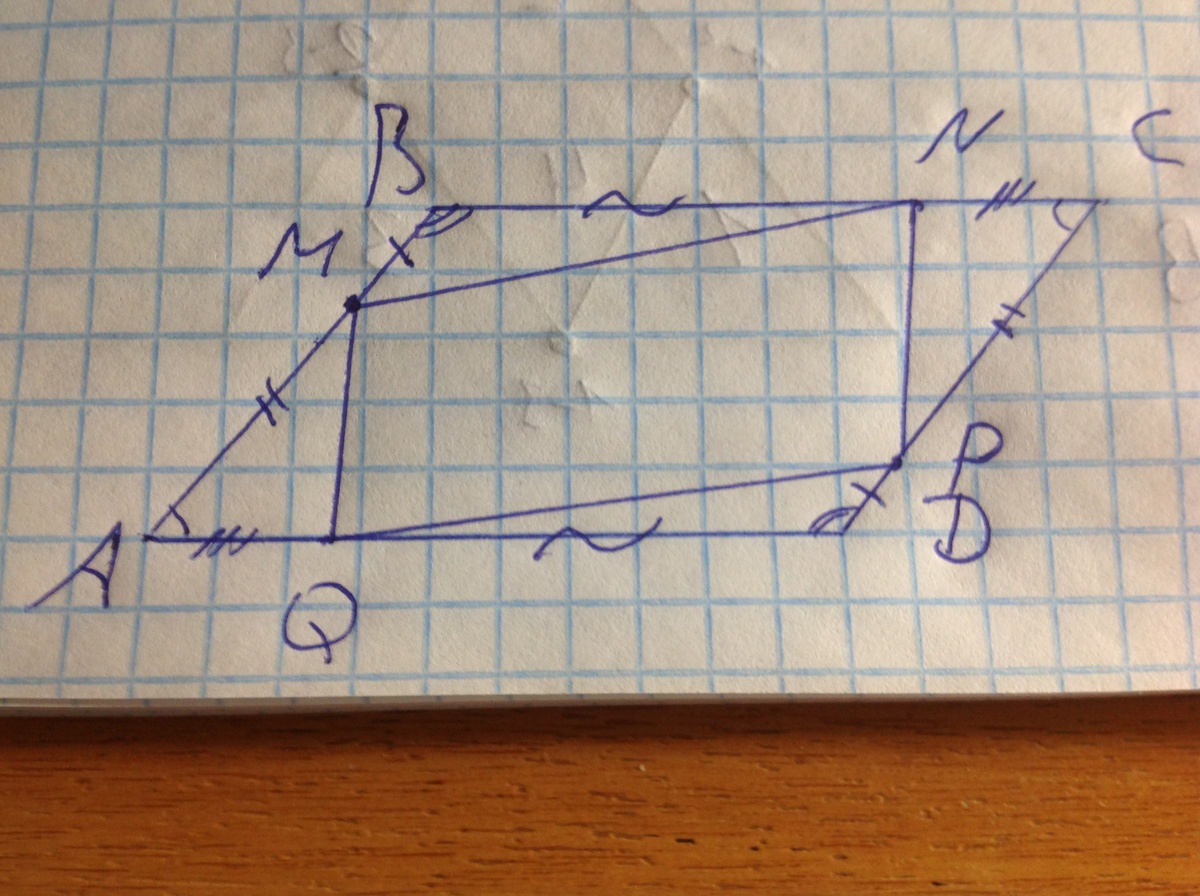
На сторонах AB,BC,CD,DA четырёхугольника ABCD отмечены соответственно точки M,N,P,Q так,что AM=CP, BN=DQ, BM=DP, NC=QA. Докажите,что ABCD и MNPQ ---ПАРАЛЛЕЛОГРАММЫ.
Ответы
Автор ответа:
0
Заметим, что AB=AM+BM, CD=CP+DP, BC=BN+CN, AD=AQ+DQ.
По условию, AM=CP, BM=DP, тогда AB=CD. Также BN=DQ, CN=AQ, тогда BC=AD. Противоположные стороны четырехугольника ABCD попарно равны, тогда этот четырехугольник - параллелограмм.
В параллелограмме противоположные углы попарно равны. Рассмотрим треугольники AMQ и CNP. Они равны по 2 сторонам и углу между ними. Тогда MQ=NP. Аналогично, треугольники BMN и OPQ равны по 2 сторонам и углу между ними, тогда MN=PQ. В четырехугольнике MNPQ противоположные стороны попарно равны, тогда этот четырехугольник также является параллелограммом.
По условию, AM=CP, BM=DP, тогда AB=CD. Также BN=DQ, CN=AQ, тогда BC=AD. Противоположные стороны четырехугольника ABCD попарно равны, тогда этот четырехугольник - параллелограмм.
В параллелограмме противоположные углы попарно равны. Рассмотрим треугольники AMQ и CNP. Они равны по 2 сторонам и углу между ними. Тогда MQ=NP. Аналогично, треугольники BMN и OPQ равны по 2 сторонам и углу между ними, тогда MN=PQ. В четырехугольнике MNPQ противоположные стороны попарно равны, тогда этот четырехугольник также является параллелограммом.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Armi06
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: xgjo
Предмет: Математика,
автор: OlgaKuzina201
Предмет: География,
автор: msyaan