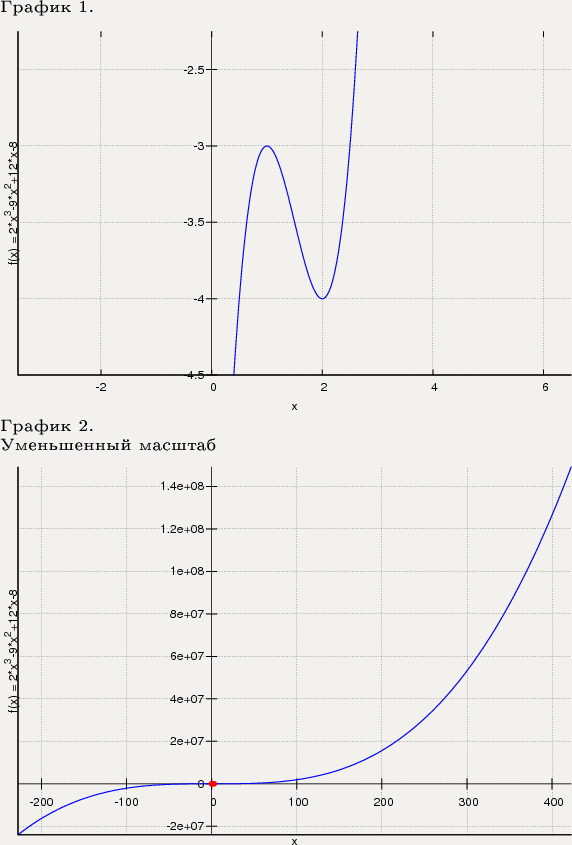
Исследовать функцию и построить график
f(x)=2x^3-9x^2+12x-8
Ответы
f(x)=2x^3-9x^2+12x-8
Область определения функции:
х∈(-∞,∞)
Пересечение с осью абсцисс (ОХ):
2х∧3-9х∧2+12х-8=0⇔х=(4√3+7)∧1/3/2+1/2*(4√3+7)∧1/3+3/2
Пересечение с осью ординат (ОУ):
х=0, f(x)=-8
Поведение функции на бесконечности:
Limx->∞2х∧3-9х∧2+12х-8=∞
Limх->-∞2х∧3-9х∧2+12х-8=-∞
Исследование функции на четность/нечетность:
f(x)=2х∧3-9х∧2+12х-8
f(-x)=-2х∧3-9х∧2-12х-8
Функция не является ни четной, ни ничетной.
Производная функции:
d/dx(2x∧3-9х∧2+12х-8)
2(d/dx(x∧3))-9(d/dx(x∧2))+12(d/dx(x))+d/dx(-8)
2(d/dx(x∧3))-9(d/dx(x∧2))+12(d/dx(x))+0
2(d/dx(x∧3))-9(d/dx(x∧2))+1*12
2(d/dx(x∧3))-9(2x)+12
2(3x∧2)-18x+12
6x∧2-18x+12
Нули производной:
х=1
х=2
Функция возрастает на:
х∈(-∞,1]U[2,∞)
Функция убывет на:
х∈[1,2]
Минимальное значение функции: -∞
Максимальное значение функции: ∞
График: