ПРОШУ ПОМОГИТЕ
Три точки А, В и С расположены так, что вектор ВС = 1/2 вектора АВ.
Докажите, что для любой точки О справедливо равенство: вектор ОВ = 1/3 вектора ОА + 2/3 вектора ОС.
Ответы
Ответ:
Доказательство в объяснении.
Объяснение:
Определение: "Произведением ненулевого вектора АВ на число n является такой вектор b, длина которого равна |n|*|a|, причём векторы a и b сонаправлены (направлены в одну сторону) при n>= 0".
В нашем случае вектор ВС = (1/2)·АВ, то есть вектор ВС направлен в одну сторону, что и вектор АВ. А так как началом вектора ВС является конец вектора АВ, значит они лежат на одной прямой.
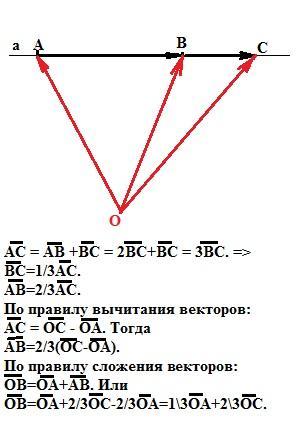
Откладываем на прямой "а" векторы АВ и ВС. Берем любую точку О и соединяем точку о с точками А, В и С. Получили векторы ОА, ОВ и ОС.
Вектор АС = АВ +ВС = 2ВС+ВС = 3ВС. => ВС=1/3АС.
АВ=2/3АС.
По правилу вычитания векторов: АС = ОС - ОА. Тогда
АВ=2/3(ОС-ОА).
По правилу сложения векторов: ОВ=ОА+АВ. Или
ОВ=ОА+2/3ОС-2/3ОА=13ОА+23ОС.
Что и требовалось доказать.