Question

Найти множество значений функции:

y=cos 4x cos 3x + sin 4x sin 3x - 5

y=(sinx+cosx)^2

y=2x-1/x-2(в дан.случае кроме чисел :__)

Answer 1

Вот прикрепил как делать первый пример...

Answer 2

$y=cos 4xcos 3x+sin 4xsin 3x-5=cos (4x-3x)-5=cos x-5$

Функция y = cosx изменяется в пределах от -1 до 1. Оценим в виде двойного неравенства

$-1leqcos xleq1~~~~big|-5\ -1-5leqcos x-5leq1-5\ -6leq cos x-5leq-4$

Множество значений функции $E(y)=[-6;-4]$

$y=(sin x+cos x)^2=1+sin 2x$

Множество значений функции sin 2x - [-1;1]. Аналогично, оцениваем в виде двойного неравенства

$-1leqsin 2xleq1~~~|+1\ 1-1leq1+sin 2xleq1+1\ 0leq 1+sin 2xleq2$

Множество значений функции: $E(y)=[0;2].$

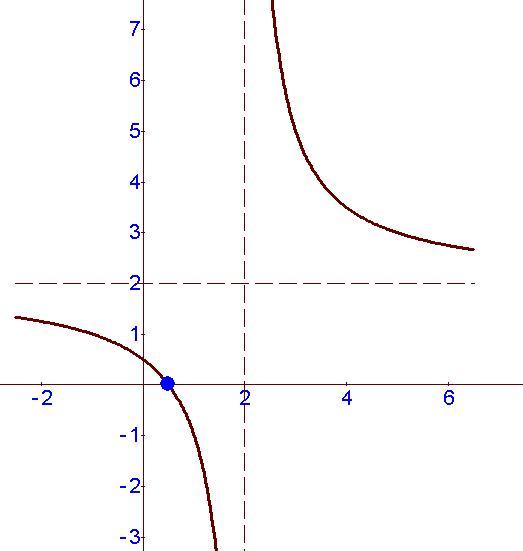
Графиком функции является гипербола. Переходя к пределу при х стремящихся к бесконечности горизонтальная асимптота функции

$y=displaystyle lim_{x to infty}dfrac{2x-1}{x-2}=2$

Область значений функции : $E(y)=(-infty;2)cup (2;+infty)$