Question

в прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 . определить площадь треугольника.

Answer 1

Обозначим данный треугольник АВС, 

∠С=90°, ВК- биссектриса, СК=4, КА=5.

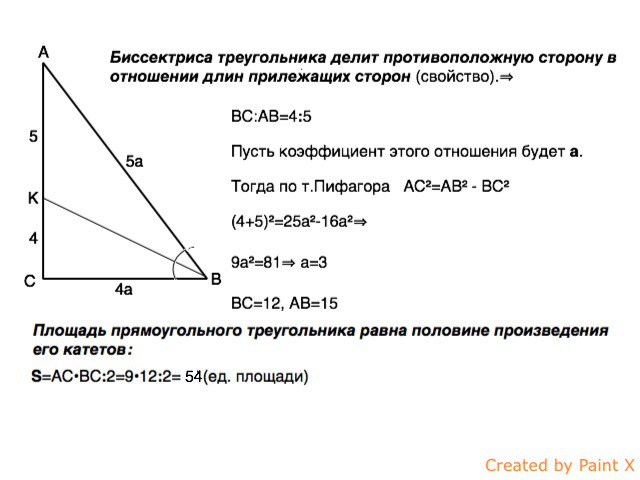
 Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон (свойство).⇒

ВС:АВ=4:5

Пусть коэффициент этого отношения будет а. 

Тогда по т.Пифагора 

АС²=АВ² - ВС²

(4+5)²=25а²-16а²⇒

9а²=81⇒

а=3

ВС=12, АВ=15

Площадь прямоугольного треугольника равна половине произведения катетов: 

S=АC•ВC:2=9•12:2=54 (ед. площади)