Предмет: Геометрия,
автор: Аноним
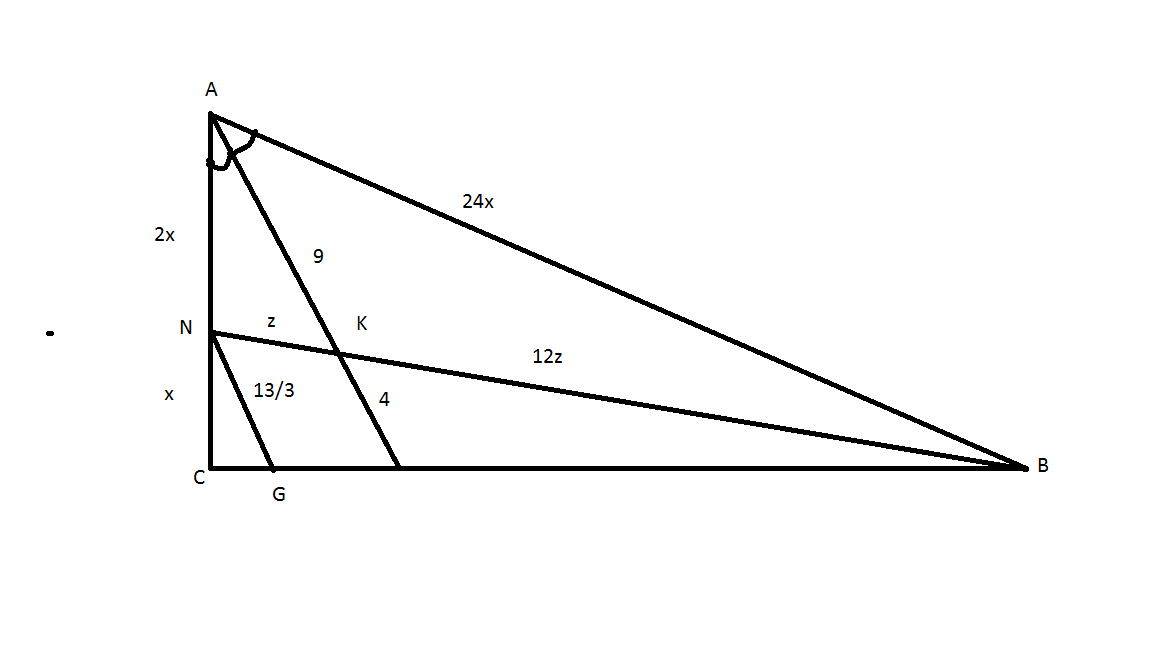
В прямоугольном треугольнике АВС с гипотенузой АВ точка N делит катет АС в отношении 2:1 считая от вершины А. Известно, что отрезок ВN пересекает биссектрису АМ в точке К так, что АК=9, КМ =4. Найти стороны треугольника АВС.
Ответы
Автор ответа:
0
Опустим NG||AM CAM и СNG подобны: NG=13/3
NGB и KAB подобны: NK/KB=1/12
ПО теореме бессектрисы: AB=24x
СB=8*CN
Далее по пифагору:
x*sqrt(24^2-9)=sqrt(169-9x^2)*8
Дальше сами.
NGB и KAB подобны: NK/KB=1/12
ПО теореме бессектрисы: AB=24x
СB=8*CN
Далее по пифагору:
x*sqrt(24^2-9)=sqrt(169-9x^2)*8
Дальше сами.
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: kamilyaahmetowa
Предмет: История,
автор: SchoolinMadrid
Предмет: Другие предметы,
автор: tron29929
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: УМНОСТЬ