Расстояние между двумя станциями метро S=3 км поезд проходит со средней скорость 54 км/ч. При этом на разгон он тратит 20 секунд, а затем некоторе время идет равномерно и на торможение до полной остановки тратит 10 секунд. Постройте график скорости движения поезда и определите наибольшую скорость поезда, его ускорение на первом участке пути и длину первого участка.
Ответы
Средняя скорость v = 54 км/час = 15 м/сек
Время движения между станциями t = S/v = 3000/15 = 200 сек
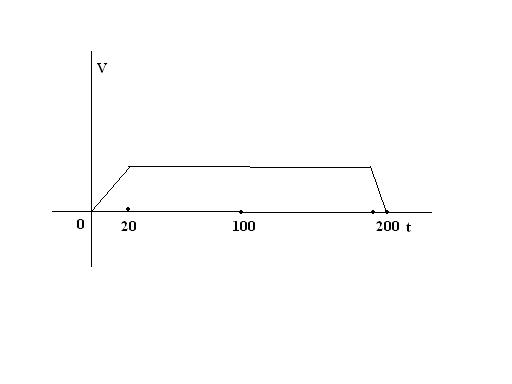
График выглядит так: сначала линейно возрастает, потом скорость постоянна, потом убывает до нуля. Первый участок = 20 сек, горизонтальный - 170сек, убывающий - 10сек (см рисунок)
Средняя скорость на 1 и последнем участках = (0+V)/2
Путь между станциями S = (0+V)*20/2 + 170*V + (V+0)*10/2 = 10V+170V+5V = 185V = 3000
Vmax = 3000/185 ≈ 16,2 м/сек
a = V/t = 16,2/20 ≈ 0,8 м/сек²
s = [16,2/2]*20 = 8,1*20 = 162 м
Ответ:
Объяснение:
Дано:
s = 3 км = 3000 м
< v > = 54 км/ч = 15 м/с
t1 = 20 c
t2 = 10 c
----------------------------------------
v( max ) - ?
a1 - ?
s1 - ?
Решение:
< v > = s/( t1 + t2 + t3 )
Где t2 - время движения поезда на втором участке
t1 + t2 + t3 = s/< v >
t3 = s/< v > - ( t2 + t3)
t3 = 3000/15 - ( 10 + 20 ) = 170 c
Также
s = s1 + s2 + s3
s = ( ( v0 + v( max ) )t1 )/2 + v( max )t2 + ( ( v( max ) + v )t1 )/2
Где v0 ; v - начальная и конечная скорость поезда на всем пути соответственно ( v0 = v = 0 м/с )
s = ( v( max )t1 )/2 + v( max )t2 + ( v( max )t1 )/2
2s = v( max )t1 + 2v( max )t2 + v( max )t1
2s = v( max )( t1 + 2t2 + t1 )
v( max ) = ( 2s )/( t1 + 2t2 + t1 )
v( max ) = ( 2 * 3000 )/( 20 + 2 * 170 + 10 ) ≈ 16,2 м/с
а1 = ( v( max ) - v0 )/t1
Т.к. v0 = 0 м/с
а1 = v( max )/t1
а1 = 16,2/20 ≈ 0,81 м/с²
s1 = v0t + ( a1t1² )/2
Т.к. v0 = 0 м/с
s1 = ( a1t1² )/2
s1 = ( 0,81 * 20² )/2 = 162 м
( Какой именно график надо чертить в условии не сказано ( скорее всего v(t) поэтому его я и начерчу ) )
