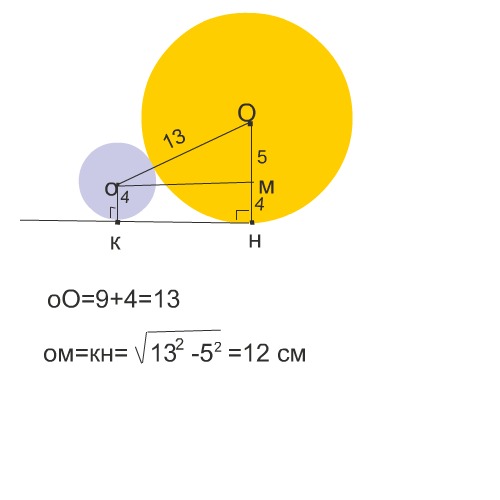
Круга, радиус которых равны 4см и 9см, имеют внешний ощупь. К кругам проведенной общую внешнюю дотичную. Найдите расстояние между точками соприкосновения.
Ответы
Расстояние между центрами окружностей
4 + 9 = 13см
разность радиусов
9 - 4 = 5см
Прямоугольный тр-к с гипотенузой, равной расстоянию между центрами 13см, и катетами, равными: 1-й - расстоянию между точками касания - х, 2-й разности радиусов 5см, решается по теореме Пифагора
13² = 5² + х²
х² + 169 - 25 = 144
х = 12
Очень все просто, если сделать рисунок.
Соединим центры кругов с точками касания и проведем из центра меньшего круга прямую, параллельную касательной, до пересечения с радиусом большего круга. Отрезок этой прямой равен расстоянию между точками касания. Соединив радиусы этих кругов, получим прямоугольный треугольник. Гипотенуза в нем равна сумме радиусов, меньший катет - разности между радиусами.
По теореме Пифагора найдем больший катет, который равен расстоянию между точками касания.
Он равен √(169-25)=12 см.
Если помните некоторые из Пифагоровых троек, то можно обойтись без вычисления. Эта тройка 5,12,13
(Пифагорово число (пифагорова тройка) — комбинация из трёх целых чисел , удовлетворяющих соотношению Пифагора. Простейший из них — египетский треугольник со сторонами 3, 4 и 5
См. рисунок.