Предмет: Алгебра,
автор: soltsolt2014
Напишите уравнение касательной к графику функции f'(x)=2-1/x в точке с абсциссой в точке x нулевое=0,5.
Ответы
Автор ответа:
0
Нам задано производную функции f'(x)=2-1/x. Для составления уравнения касательной нужно иметь саму функцию, поэтому f(x)=Int(2-1/x)=2x-ln(x)+C.
Значение функции f(1/2)=1+ln2+C (С можно принимать какое угодно число, примем С=0). Значение производной f'(1/2)=0. Тогда уравнение касательной запишется: y-(1+ln2)=0(x-1/2), y=1+ln2-уравнение касательной.
Если принять С=1, то уравнение касательной будет иметь вид y=2+ln2. Но тогда и функция будет иметь вид f(x)=2x-ln(x)+1. И т.д.
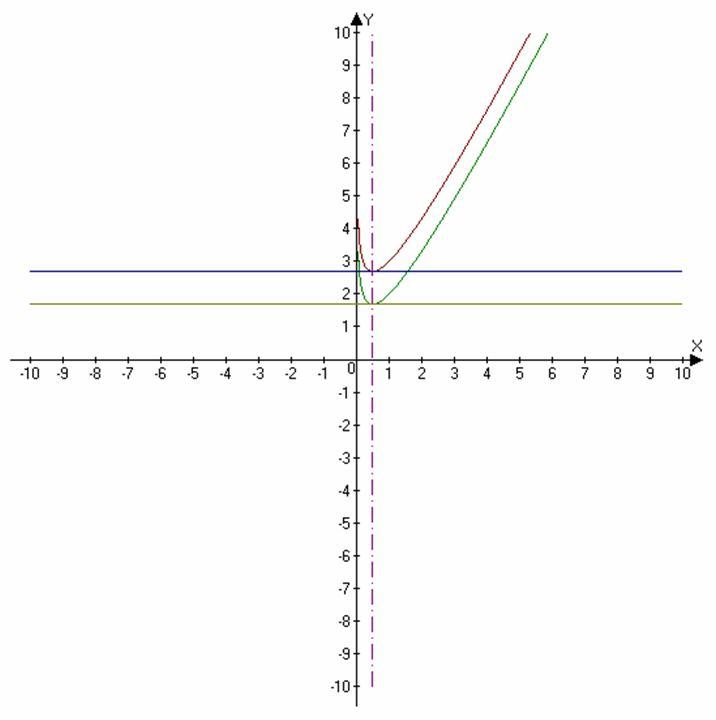
Даю примеры графиков этих функций и касательных в точке х0=0,5.
Значение функции f(1/2)=1+ln2+C (С можно принимать какое угодно число, примем С=0). Значение производной f'(1/2)=0. Тогда уравнение касательной запишется: y-(1+ln2)=0(x-1/2), y=1+ln2-уравнение касательной.
Если принять С=1, то уравнение касательной будет иметь вид y=2+ln2. Но тогда и функция будет иметь вид f(x)=2x-ln(x)+1. И т.д.
Даю примеры графиков этих функций и касательных в точке х0=0,5.
Приложения:
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Алгебра,
автор: MrDarsy
Предмет: Математика,
автор: igrokwarface
Предмет: Математика,
автор: bxtecv089