Предмет: Алгебра,
автор: Артур998
Решите номер 30.Есть вложение.
Приложения:
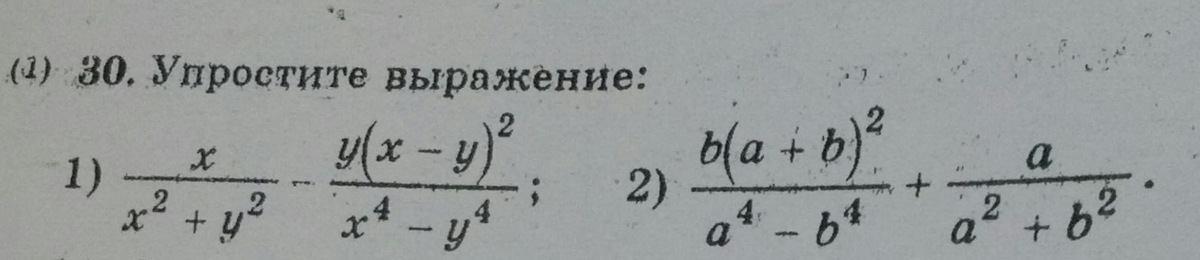
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: ksntabanova
Предмет: Алгебра,
автор: alpysniara
Предмет: Информатика,
автор: zhzhzhzhzhzhzhzh
Предмет: Литература,
автор: Ablai97
Предмет: Химия,
автор: shajshdh