Предмет: Геометрия,
автор: лизухин
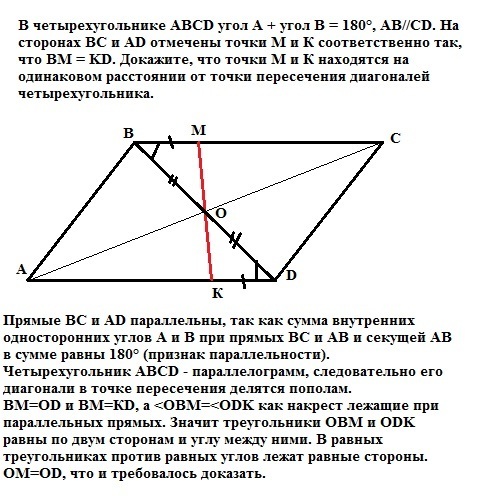
В четырехугольнике ABCD угол A + угол B = 180°, АВ//CD. На сторонах ВС и AD отмечены точки М и К соответственно так, что ВМ = KD. Докажите, что точки М и К находятся на одинаковом расстоянии от точки пересечения диагоналей четырехугольника.
Ответы
Автор ответа:
0
Прямые ВС и АD параллельны, так как сумма внутренних односторонних углов А и В при прямых ВС и АВ и секущей АВ в сумме равны 180° (признак параллельности).
Четырехугольник АВСD - параллелограмм, следовательно его диагонали в точке пересечения делятся пополам.
ВМ=ОD и ВМ=КD, а <OBM=<ODK как накрест лежащие при параллельных прямых. Значит треугольники ОВМ и ОDK равны по двум сторонам и углу между ними. В равных треугольниках против равных углов лежат равные стороны.
ОМ=ОD, что и требовалось доказать.
Четырехугольник АВСD - параллелограмм, следовательно его диагонали в точке пересечения делятся пополам.
ВМ=ОD и ВМ=КD, а <OBM=<ODK как накрест лежащие при параллельных прямых. Значит треугольники ОВМ и ОDK равны по двум сторонам и углу между ними. В равных треугольниках против равных углов лежат равные стороны.
ОМ=ОD, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: История,
автор: polinaross06
Предмет: Математика,
автор: cantexnikigor
Предмет: История,
автор: sasagorbunova02
Предмет: Алгебра,
автор: daurentapenov
Предмет: Алгебра,
автор: natali7767