Предмет: Алгебра,
автор: Ablai97
Вычислите S фигуры ограниченной линиями
Приложения:
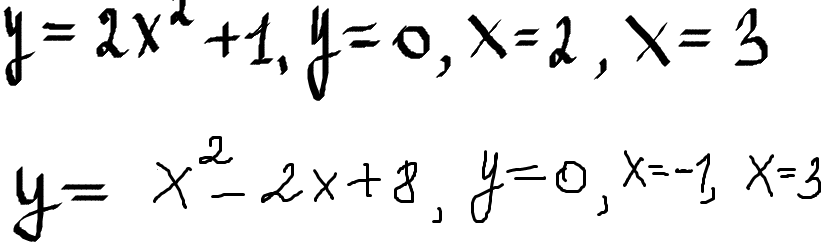
Ответы
Автор ответа:
0
1) Парабола расположена выше оси ох, поэтому

2) Так как D=(-2)²-4·8<0 парабола не пересекает ось ох

2) Так как D=(-2)²-4·8<0 парабола не пересекает ось ох
Похожие вопросы
Предмет: Русский язык,
автор: htrfghhrtf
Предмет: Физика,
автор: nurzigitmuratov4
Предмет: Математика,
автор: kristinakonina70
Предмет: Математика,
автор: gulsina196310