Предмет: Алгебра,
автор: Аноним
Оформить решение на листке. Подробно.
Приложения:
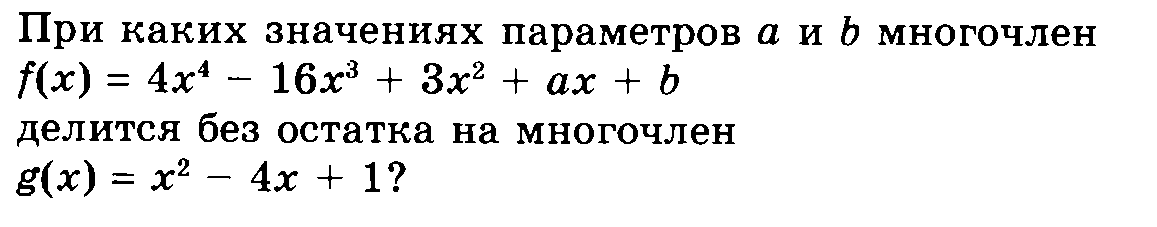
Ответы
Автор ответа:
0
4x^4-16x³+4x²-x²+ax+b=4x²(x²-4x+1)-(x²-ax-b)
следовательно (x²-ax-b) должно делиться без остатка на x²-4x+1, что возможно при а=4 и b=-1
следовательно (x²-ax-b) должно делиться без остатка на x²-4x+1, что возможно при а=4 и b=-1
Автор ответа:
0
и вам тоже спасибо
Автор ответа:
0
_4x⁴ - 16x³ + 3x² + ax + b |x²-4x+1
4x⁴- 16x³ + 4x² 4x² - 1
_-x² + ax + b
-x² +4x - 1
(a-4)x +(b+1)
Остаток (a-4)x +(b-1) должен равняться нулю.
Т.е многочлен первой степени (a-4)x +(b-1) приравниваем к многочлену первой степени
0х+0, получим систему

4x⁴- 16x³ + 4x² 4x² - 1
_-x² + ax + b
-x² +4x - 1
(a-4)x +(b+1)
Остаток (a-4)x +(b-1) должен равняться нулю.
Т.е многочлен первой степени (a-4)x +(b-1) приравниваем к многочлену первой степени
0х+0, получим систему
Автор ответа:
0
один вопрос
Автор ответа:
0
Там же написано. Остаток должен равняться нулю. Но остаток многочлен. Мы же не корень ищем. А коэффициенты.
Похожие вопросы
Предмет: Английский язык,
автор: ultchurai
Предмет: Математика,
автор: olgbatrakov
Предмет: Химия,
автор: gamemr594
Предмет: Математика,
автор: Layha