Question

В прямоугольном треугольнике АВС с прямым углом В, проведены ВН – высота, АМ – медиана, которые пересекаются в точке Р. Определить длину АВ, если ВР=10, РН=2.

Answer 1

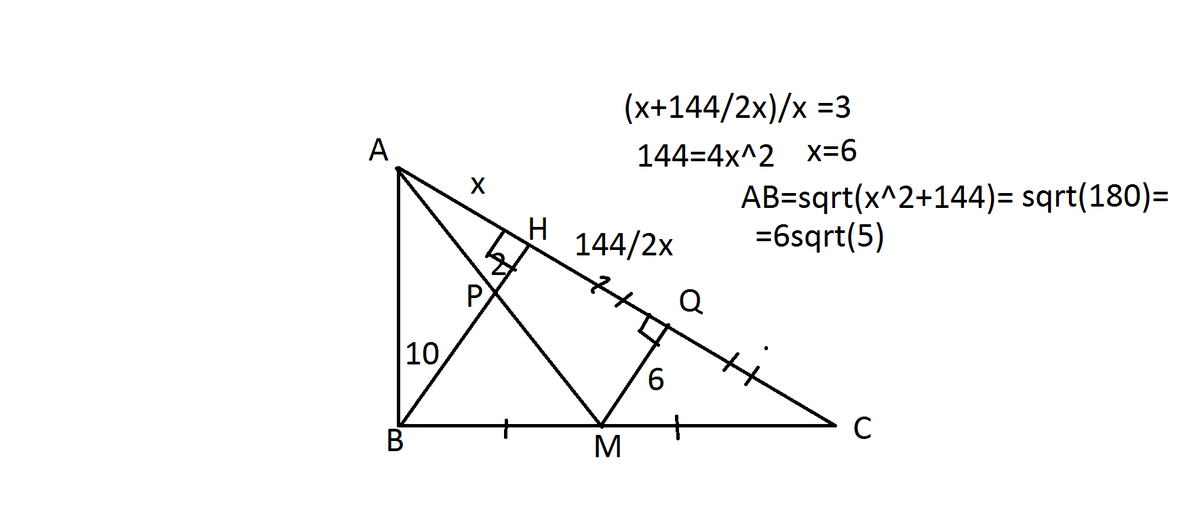
Проведем перпендикуляр MQ||BH||PH. То  MQ-cредняя  линия  треугольника BHC.  MQ=BH/2=6. (HQ=QC)  
Треугольники  AMQ и APH подобны. 
По  теореме  высоты: AH*HC=144
то если  AH=x  HC=144/x , HQ=144/2x
Далее  все на  рисунке.
Ответ:6sqrt(5)