Question

диагонали прямоугольника пересекаются под углом 60 градусов. Длина диагонали равна 12.Найдите длину большей стороны прямоугольника

Answer 1

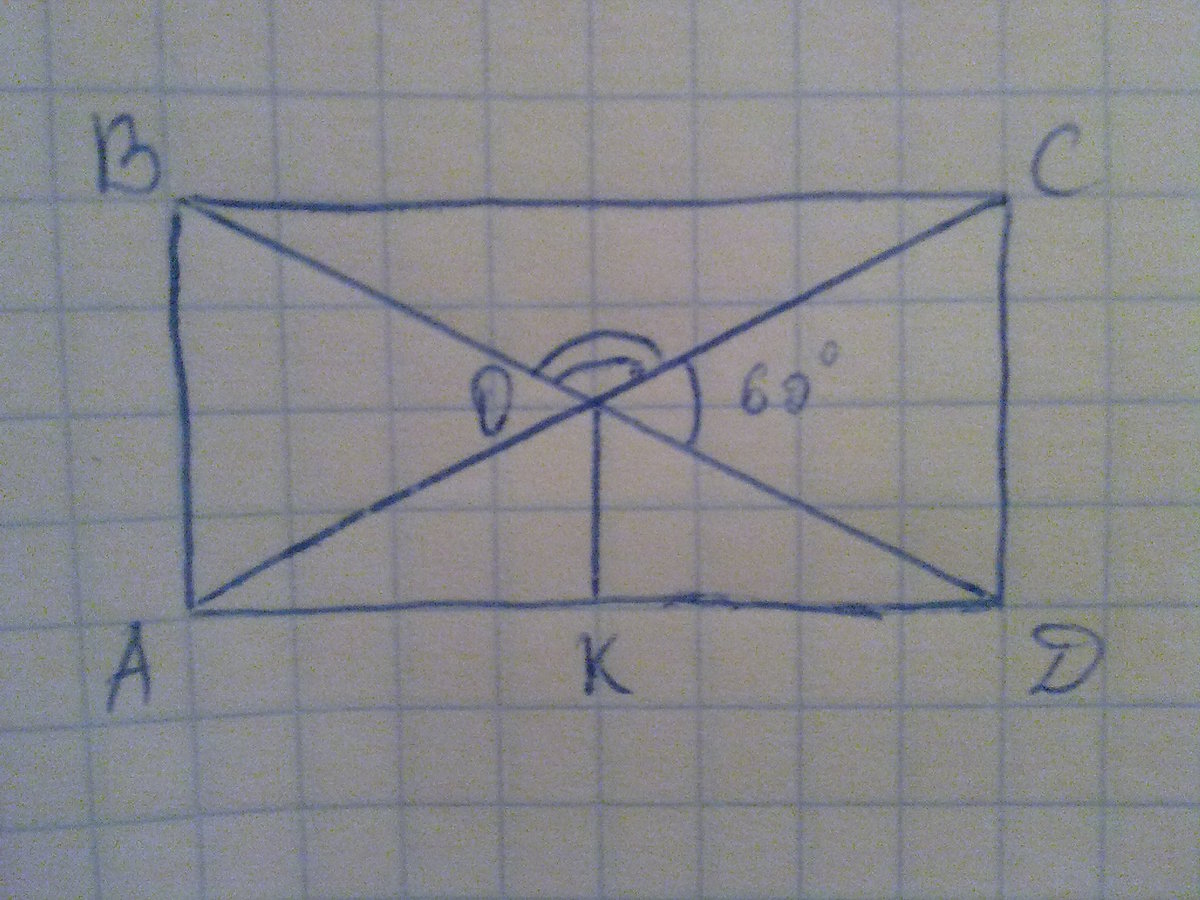
Дано прямоугольник ABCD, O - точка пересечения диагоналей прямоугольника, угол СOD = 60 градусов, АС = ВD = 12.

 

Так как угол СOD = углу ВОА = 60 градусов, то угол ВСО = углу АОD = (360 - (60 + 60))/2 = (360 - 120)/2 = 240/2 = 120 градусов.

Проведем на сторону АD высоту ОК, которая будет и медианой и биссектрисой, так как треугольник АОD  равнобедренный. Треугольник ОКD  - прямоугольный. Выходя из того, что ОК - биссектриса, угол КОD = угол АОD/2 = 120/2 = 60 градусов. Гипотенуза ОD  = ВD/2 = 12/2.

sin KOD = KD/OD , отсюда КD = ОD*sin KOD = 6*sin 60 = 6*√3/2 = 3√3.

Так как АК = КD, то АD = АК + КD = 3√3 + 3√3 = 6√3 .