Предмет: Геометрия,
автор: TAO
Прямоугольный треугольник с катетами 9 см и 12 см вписан в окружность. Найдите ее радиус.
Ответы
Автор ответа:
0
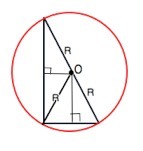
Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.
По т.Пифагора с²=a²+b², где с - гипотенуза, a и b – катеты.
с=√(9²+12²)=15
R=15:2=7,5 см
Подробно.
Центр описанной окружности треугольника лежит на пересечении срединных перпендикуляров к его сторонам.
Срединные перпендикуляры прямоугольного треугольника пересекаются на середине гипотенузы, следовательно центр описанной окружности - середина гипотенузы, и радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. R=7,5 см.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: dgopaleksei548
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: aluadutbaeva
Предмет: Физика,
автор: Кашапова14