Question

Очень надо!!!!
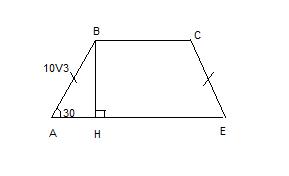
Боковая сторона равнобочной трапеции равна 10√3 см, а острый угол - 30 градусов. Найдите площадь этой трапеции, если известно, что в нее можно вписать окружность.

Answer 1

1. S=(AE+BC):2 * BH
2. Т.к. по условию в трапецию можно вписать окружность, то сумма ее противоположных сторон должна быть равна (в любом описанном четырехугольнике суммы противоположных сторон равны). Значит
АЕ+ВС=АВ+СЕ=20√3 cм
3. Рассмотрим прямоугольный треуг-ик АНВ, полученный после построения высоты ВН. Здесь катет ВН лежит против угла в 30°, значит, он равен половине гипотенузы АВ:
ВН=1/2АВ=5√3 см
4. В формулу площади подставим сумму АЕ и ВС (п.2) и высоту:
S=20√3:2 * 5√3=50*3=150 см²