Предмет: Геометрия,
автор: supernastea98
в прямоугольном треугольнике abc угол c 90,AC=2,BC=4^2.Найти длину высоты треугольника,проведенной к гипотенузе
Ответы
Автор ответа:
0
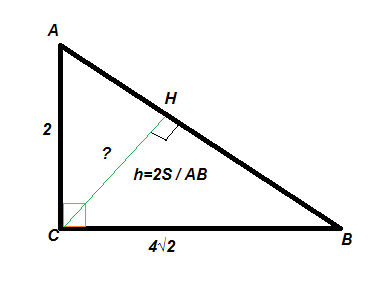
Дано: АВС = прямоугольный треугольник, ∠С=90°, АС= 2, ВС=4√2.
Найти: CH
Решение:
По т. Пифагора определим гипотенузу

Площадь прямоугольного треугольника равна произведение катетов разделить на 2

Итак, высота СН равна:

Ответ:
Найти: CH
Решение:
По т. Пифагора определим гипотенузу
Площадь прямоугольного треугольника равна произведение катетов разделить на 2
Итак, высота СН равна:
Ответ:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: keldybajerasyl
Предмет: Українська мова,
автор: gooseonthetitle
Предмет: Химия,
автор: ViktorHee
Предмет: Алгебра,
автор: Аноним