Предмет: Геометрия,
автор: сашуляка1998
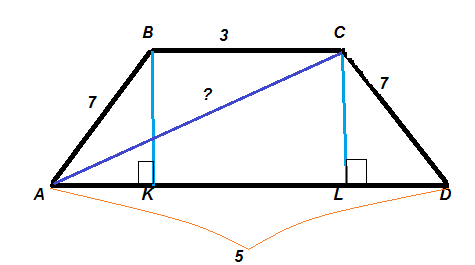
В равнобедренной трапеции основания равны 3 см и 5 см а боковая сторона равна 7см Вычислите диагонали и площадь трапеции
Ответы
Автор ответа:
0
Дано: ABCD - равнобедренная трапеция, ВС =3см, AD=5см,АВ = CD = 7см.
Найти: и
и 
Решение:
У равнобедренной трапеции боковые стороны и углы при основания равны. Диагонали равнобедренной трапеции также равны.
С прямоугольного треугольника CDL (∠CLD = 90°):
АК = LD =
По т. Пифагора определим высоту CL

Тогда площадь равнобедренной трапеции равна:

Тогда диагональ по т. Пифагора

Ответ:
Найти:
Решение:
У равнобедренной трапеции боковые стороны и углы при основания равны. Диагонали равнобедренной трапеции также равны.
С прямоугольного треугольника CDL (∠CLD = 90°):
АК = LD =
По т. Пифагора определим высоту CL
Тогда площадь равнобедренной трапеции равна:
Тогда диагональ по т. Пифагора
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: nazirayegizbayeva
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: zakipovadiana876
Предмет: Математика,
автор: АринаСильченко
Предмет: Биология,
автор: Аноним