Предмет: Алгебра,
автор: Arinak98
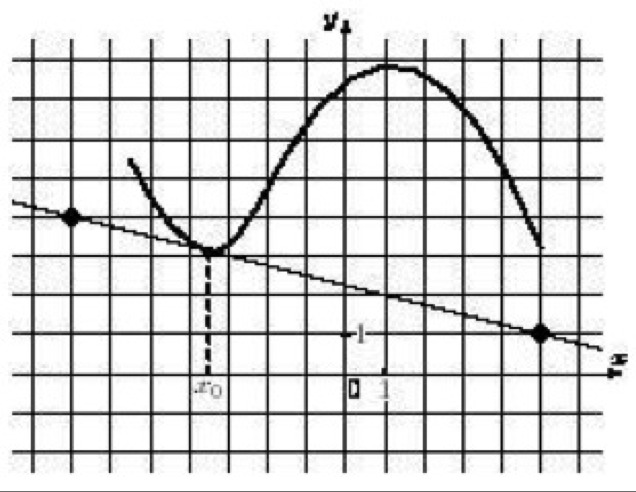
На рисунке изображены график функции y=f (x) и касательная
к нему в точке с абсциссой x0 . Найдите значение производной функции f (x) в точке x0
Приложения:
Ответы
Автор ответа:
0
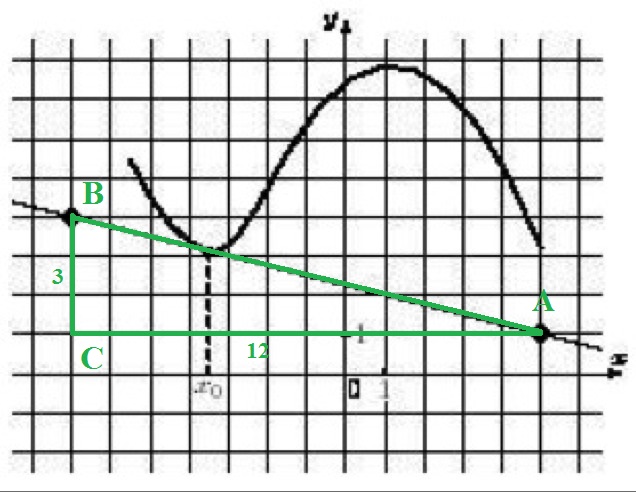
Геометрический смысл производной в точке – это тангенс угла наклона касательной.
На графике отмечен равнобедренный треугольник (один из многих, которые характеризуют угол наклона касательной к графику с отрицательным направлением оси абсцисс).
(один из многих, которые характеризуют угол наклона касательной к графику с отрицательным направлением оси абсцисс).
Т.е. в равнобедренном треугольнике стороны подчиняются следующим соотношениям:

В нашем , следовательно:
, следовательно:

Единственно, это угол, который касательная образует с отрицательным направлением оси абсцисс. Угол, который она образует с положительной будет равен:

На графике отмечен равнобедренный треугольник
Т.е. в равнобедренном треугольнике стороны подчиняются следующим соотношениям:
В нашем
Единственно, это угол, который касательная образует с отрицательным направлением оси абсцисс. Угол, который она образует с положительной будет равен:
Приложения:
Автор ответа:
0
Если не видно формул, обновите страницу. Если есть вопросы, задавайте в личных сообщениях или в комментариях к решению.
Похожие вопросы
Предмет: Математика,
автор: nn6957313
Предмет: Математика,
автор: JKT20132020
Предмет: Математика,
автор: amalchievaruzama
Предмет: Обществознание,
автор: lotos1404
Предмет: Химия,
автор: assasin199712