Предмет: Геометрия,
автор: атол
СРОЧНО ПОЖАЛУЙСТА 65 БАЛОВ ПОМОГИТЕ!!!
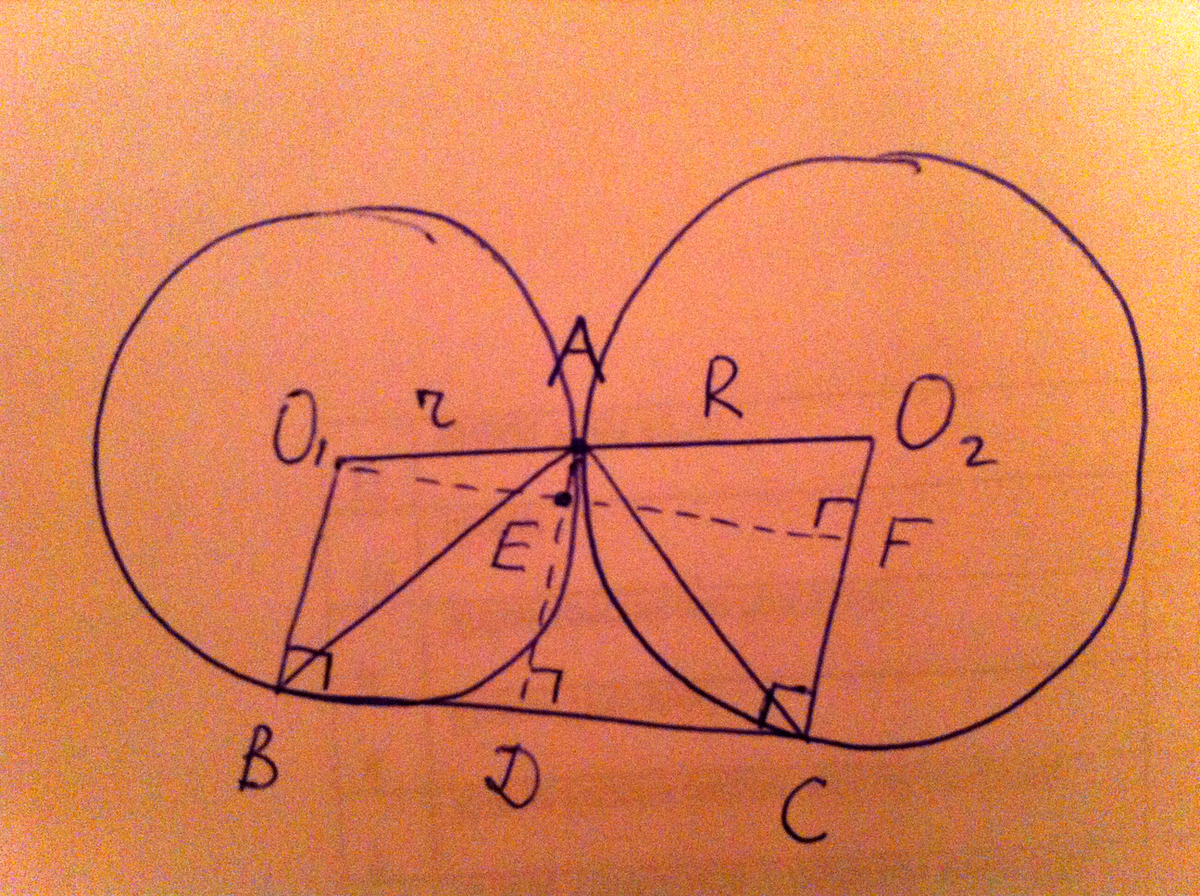
К двум окружностям с центрами в точках О1 и О2, касающимся внешним образом в точке А, проведена общая касательная ВС (В и С – точки касания). Докажите, что угол ВАС – прямой.
Ответы
Автор ответа:
0
AD -- перпендикуляр к BC.
O₁F -- перпендикуляр к O₂C.
O₁O₂ = r + R, O₂F = R - r
O₁F =
ВС = O₁F =2
BD = BC·
DC = BC·
ΔO₁AE подобен ΔO₁O₂F, поэтому

AD = AE + ED =
Если <BAC -- прямой, тогда длина высоты AD должна быть равна среднему геометрическому длин отрезков BD и DC, на которые она разбивает гипотенузу BC.
Убедимся, что: AD =


<BAC -- действительно прямой.
См. рис. в прилагаемом файле.
O₁F -- перпендикуляр к O₂C.
O₁O₂ = r + R, O₂F = R - r
O₁F =
ВС = O₁F =2
BD = BC·
DC = BC·
ΔO₁AE подобен ΔO₁O₂F, поэтому
AD = AE + ED =
Если <BAC -- прямой, тогда длина высоты AD должна быть равна среднему геометрическому длин отрезков BD и DC, на которые она разбивает гипотенузу BC.
Убедимся, что: AD =
<BAC -- действительно прямой.
См. рис. в прилагаемом файле.
Приложения:
Похожие вопросы
Предмет: Физика,
автор: ademikumenova176
Предмет: Информатика,
автор: merkulovsasa49
Предмет: Алгебра,
автор: zara2107
Предмет: История,
автор: kiritokun28
Предмет: География,
автор: маргарита2602