Question

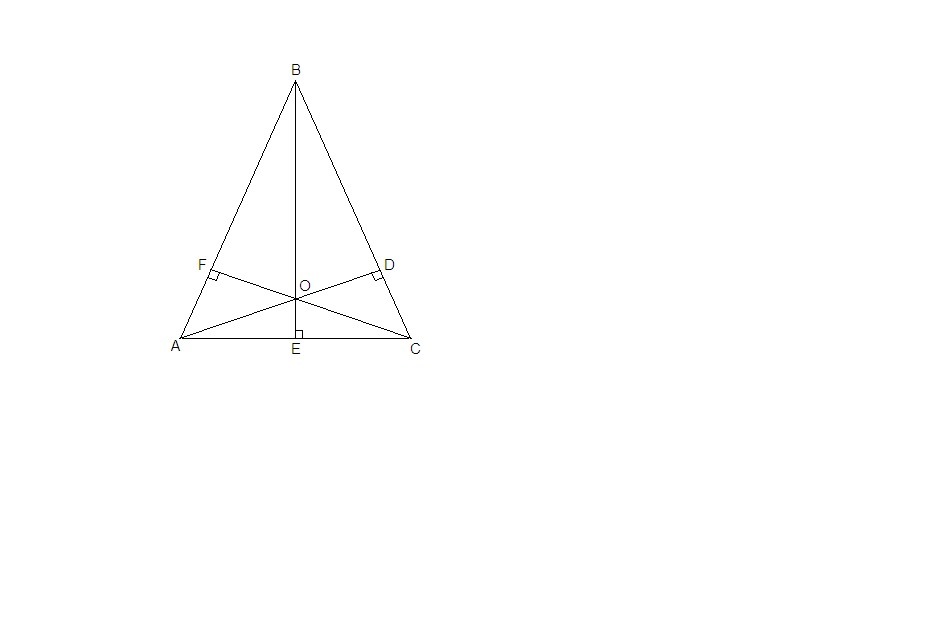
высоты треугольника АВС пересекаются в точке О, причём угол АОВ= угол СОВ=110 градусам.
а) Докажите, что АВС равнобедренный и найдите его боковые стороны
б) найдите угла данного треугольника

Answer 1

а)
 ∠АОВ = ∠СОВ = 110°, значит
∠AOE = ∠COE = 180° - 110° = 70° как углы, смежные с равными углами
 
В треугольнике АОС OE является высотой и биссектрисой, значит ΔАОС равнобедренный, ⇒

АО = ОС,
∠АОВ = ∠СОВ - по условию,
ОВ - общая сторона для треугольников АОВ и  СОВ, следовательно
ΔАОВ = ΔСОВ по двум сторонам и углу между ними. ⇒

АВ = ВС, т.е. ΔАВС равнобедренный.

Найти длины боковых сторон по таким данным невозможно.

б)
 ∠BOD = ∠AOE = 70° как вертикальные
ΔBOD: ∠ОВD = 180° - 90° - 70° = 20°.

Так как ΔАВС равнобедренный, BE - высота и биссектриса, значит
∠АВС = 2·∠ОВD = 40°.

∠ВАС = ∠ВСА = (180° - 40°)/2 = 70° так как углы при основании равнобедренного треугольника равны.

Ответ: 40°, 70°, 70°.