Question

Определить скорость, с которой движется тень Луны по земной поверхности во время полного солнечного затмения, если оно налбюдается на экваторе. Для простоты считать, что Солнце, Земля и Луна находятся в одной плоскости, а земная ось к этой плоскости перпендикулярна. Скорость света считать бесконечно большой по сравнению со всеми остальными скоростями. Радиус луной орбиты R=3,8.10^5 км

Answer 1

Так как не сказано где мы считаем скорость тени, то я буду считать ее на экваторе. Будем работать в система отсчета, в которой Земля покоится.

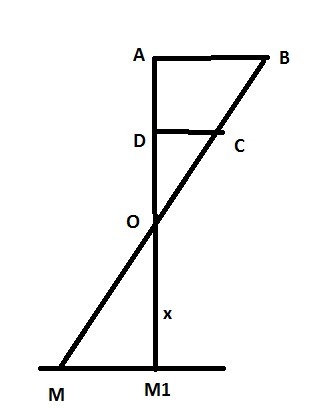
За 1 секунды Солнце и Луна переместятся с востока на запад на расстояние $AB=w_{c}R_{c}$  и $DC=w_{l}R_{l}$ . Поясняющий рисунок см в приложении. (наблюдаем в точке M1)

wc и wl-угловые скорости вращения Солнца и Луны вокруг центра Земли. Они нам кстати известны.

По сути MM1-это и есть скорость тени Луны.

Из подобиев трегольников видно, что искомая скорость $V=w_{c}*x$ (если положим, что OA=Rc, ну так как расстояние до Луны очень мало по сравнению с расстоянием до Солнца.)

Нам нужно найти x, для этого опять же воспользуемся подобиями треугольников

$frac{w_{c}R_{c}}{w_{l}R_{l}}= frac{AB}{DC} =frac{OA}{OD}$

$OD=R_{l}-x-r$ (где r-радиус Земли)

$x=frac{w_{c}-w_{l}}{w_{c}} (R_{l}-r)$

$V=w_{c}x=(w_{c}-w_{l})R_{l}-w_{c}r=frac{2pi R_{l}}{T_{m}} -frac{2pi r}{T_{c}} =frac{2*3.14*3.8*10^{5}}{27.3*86400}- frac{2*3.14*6400000}{86400}=0,55$ км/с

$T_{m}=27.3T_{c}$ - продолжительность месяца. $T_{c}$ -  продолжительность суток.