Предмет: Геометрия,
автор: Stasyarep
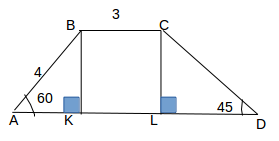
Дана трапеция с основаниями BC и AD. BC=3, AB=4,угол А=60, угол D=45.Найти площадь и периметр трапеции
Ответы
Автор ответа:
0
Дано: ABCD - трапеция, ВС = 3, АВ =4, угол А = 60градусов, угол D = 45 градусов.
Найти: и
и 
Решение:
С прямоугольного треугольника АВК (угол АКВ = 90градусов)
Косинус угла - это отношение прилежащего катета к гипотенузе, тоесть:

Синус угла это отношение противолежащего катета к гипотенузе, тоесть:

С прямоугольного треугольника DCL ( угол DLC = 90 градусов)


Осталось вычислить периметр и площадь трапеции


Ответ:
Найти:
Решение:
С прямоугольного треугольника АВК (угол АКВ = 90градусов)
Косинус угла - это отношение прилежащего катета к гипотенузе, тоесть:
Синус угла это отношение противолежащего катета к гипотенузе, тоесть:
С прямоугольного треугольника DCL ( угол DLC = 90 градусов)
Осталось вычислить периметр и площадь трапеции
Ответ:
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ZaidinInkar
Предмет: Русский язык,
автор: evelina1788
Предмет: Қазақ тiлi,
автор: viktoriakarpova12345
Предмет: Математика,
автор: lianohka