Предмет: Геометрия,
автор: nemercev26
Дано ABCD ромб, BD = 16 cm, AC = 12 cm, Найти P and S ромба.
Ответы
Автор ответа:
0
Дано: ABCD - ромб, BD = 12см, AC =12 см.
Найти: и
и 
Решение:
У ромба все стороны равны. О - точка пересечений диагоналей, делит диагоналей на отрезки пополам, тоесть:
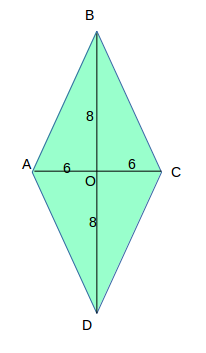
BO = DO = BD/2 = 16/2 = 8 см, AO = OC = AC/2= 12/2 = 6 см.
С прямоугольного треугольника ABO (угол AOB = 90 градусов):
по т. Пифагора определим сторону ромба АВ

Теперь осталось найти периметр и площадь ромба
Площадь ромба равна произведение диагоналей разделить на 2

А периметр ромба:

Ответ:
Найти:
Решение:
У ромба все стороны равны. О - точка пересечений диагоналей, делит диагоналей на отрезки пополам, тоесть:
BO = DO = BD/2 = 16/2 = 8 см, AO = OC = AC/2= 12/2 = 6 см.
С прямоугольного треугольника ABO (угол AOB = 90 градусов):
по т. Пифагора определим сторону ромба АВ
Теперь осталось найти периметр и площадь ромба
Площадь ромба равна произведение диагоналей разделить на 2
А периметр ромба:
Ответ:
Приложения:
Автор ответа:
0
Спасибо, это решение подойдёт под уровень знаний 9 класса?
Автор ответа:
0
Этот комментарий - часть решения. Опечатка в первой строке: BD = 16 см
Похожие вопросы
Предмет: Русский язык,
автор: dasha599193
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Taisialive11
Предмет: Математика,
автор: уррр
Предмет: Обществознание,
автор: Аноним